Chapter 6: Do You See My Dog?#
To this point, we have written code that required us to understand little more than the abstractions presented to us. Yet at times, we saw realities of the underlying machine through these abstractions. We learned, for example, that letters and symbols can be understood only if all parties agree on how they’re encoded. We also learned that network messages aren’t transmitted and received as an abstract whole but are passed around in fixed-sized buffers. This need for fixed-size buffers shouldn’t be too surprising; before the invention of email, writing a letter involved fixed-sized pieces of paper. We need to remember that computers are simply tools—wonderfully flexible tools, but tools nonetheless. And as such, they do not directly manipulate our abstract ideas, but concrete digital representations of them.
In this and the next two chapters, which will bring us to the end of Act I, I’ll introduce you to the digital world that underlies all modern computation. You will learn how computers represent the abstractions in our scripts and what this means for how we go about using computers to solve real-world problems. This will complete the foundation you need to use computation in your everyday lives.
Learning Outcomes
This chapter introduces you to the digital world that underlies all modern computation. It peeks below the useful abstractions we have relied on in the previous chapters and teaches us that computers encode everything as numbers. We’ll cover quite a bit of terminology while investigating what it takes to store a digital image and to identify objects in that image. By the chapter’s end, you will be able to do the following:
Describe the historical importance of numbers and how counting and measurement have been tied to knowledge and power [design].
Understand that computers represent aspects of our world as nothing more than arrays of numbers [CS concepts].
Work in Python with one- and two-dimensional arrays of numbers [programming skills].
Explain what is meant by the digital abstraction on which we build modern computing systems [CS concepts].
Define important terms like bit, byte, binary, and the addressing of bytes [CS concepts].
Interpret a sequence of bits and convert between different number systems, including hexadecimal [CS concepts].
Use a hexdump utility to inspect the raw contents of any file [programming skills].
Identify overflow and underflow conditions, as well as use techniques like saturation to handle them [CS concepts and design].
Create and work with digital images [design and programming skills].
Code a simple filter that, when applied to an image file, can highlight the edges of the objects in that image [CS concepts].
Numbers and knowledge. We are about to discover that computers encode everything as numbers. My electronic copy of this book’s manuscript is a bunch of numbers. The picture I took of my dog one weekend is stored as a bunch of numbers. The podcast I listened to on my morning walk and the songs my wife streamed on her run are simply a bunch of numbers. In fact, every file and every program on our computers are nothing but a long list of numbers.
That may sound very dry and unexciting, but it is also a very powerful idea. To understand why, we’re going to turn to Harvard professor and American historian Jill Lepore and her work to answer the question: What counts as knowledge?
There are many ways to attack this question, and I should be clear that Jill is not trying to enumerate everything that society has deemed to be knowledge. She’s been focused on identifying what society has historically used as the elemental unit of knowledge. In other words, what constitutes a fact, and how is it established?
Jill defines a fact as something a society establishes as true.[1] Her quest, then, is to understand how societies establish truth. Now, we humans didn’t always rely on ourselves for determining what was true. We spent a long time in what Jill calls the age of mysticism, when we believed that there were things that we could not know or, if you believe in God, that only God could know. In this age, when what was true was in dispute, people turned to trial by ordeal (or trial by combat) to allow fate or a higher power to intervene and show us what must be true. Jill reminds us that, even today, children still use this method to settle arguments of ownership. A Roshambo script implements a fairly harmless type of trial by ordeal.
This age of mysticism eventually gave way to the age of facts when, in 1215, trial by jury replaced trial by ordeal in England. In this period, truth depended on “an observed or witnessed act or thing,”[2] and the discernment of fact involved conversations held with others. No individual alone could dictate what was true, but also no higher power was needed. We mere humans could figure out what was true for ourselves. This change in mindset was highly influential, and as Jill states, “Between the thirteenth century and the nineteenth, [this approach to discerning] fact spread from law outward to science, history, and journalism.”[3]
Fast-forward to the eighteenth century, and Jill notes that societies and industries began to value numbers as much as other types of facts. If you could enumerate or measure something, and another person could make that same tally or measurement, the result could be considered a fact. More importantly, power and prestige became intertwined with numbers. For example, the US, with its constitutional mandate of a regular census count, became the first government to tie its legitimacy to the act of counting. Similarly, counting was a key metric in industrialization, and measurement was a key driver of science. Soon numbers and other statistics were what you needed to present in order to claim success in business and commerce.
Once we humans got a taste for the power of numerically based facts, we began to develop techniques and tools to count and measure everything around us with ever-increasing accuracy. Before long, those in science, business, and government found themselves working with collections of numbers too numerous for any individual to count or analyze by hand. To address this new challenge, we invented a new type of machine—the computer—to work with these large collections of numbers or what we now call data.
Jill marks the beginning of society’s transition into valuing data with the invention of modern computers in the 1950s. Fast-forward to today, and data science, which relies heavily on computation, permeates nearly every corner of our society. Through it, we extract meaningful insights and generate new knowledge. If you ask data scientists what they do, they’ll tell you that their objective is “to use data to answer questions and guide decision making.”[4] They are establishing what is true.
Given that we built our first computers to help us to crunch lots of numbers and spit out new knowledge, it’s logical that those machines store and manipulate numbers. What may be surprising, however, is that today’s computers use the same basic computer architecture, proposed by John von Neumann in 1945, as those original machines. In other words, at their most fundamental level (and behind all the abstractions we have discussed and all the apps you use), your laptop, smartphone, and smartwatch are simply processing numbers. Computers see the world as nothing but numbers.
Do you see my dog? Here’s a picture I took of my dog in May 2020.

Fig. 12 My dog, Cosmo, lying down in our yard.#
Do you see the dog in this image? Unless you’re visually impaired, of course you do. Our brains have learned over time what a dog looks like, and they help us identify dogs in the images captured by our eyes.
This image is stored in a file named cosmo.jpg. While we see a dog, when a computer opens this file, you might ask what the computer “sees.”. In particular, our new problem-to-be-solved will answer these two questions:
What is in an image file like
cosmo.jpg?What does it take for the computer to see the dog in that file?
No interpretation, please. Let’s start with the first of these two questions. When you ask a computer to open a file like cosmo.jpg, it displays a window with the image in Figure 12. Why is that?
Well, what might you, as a human, guess about the file’s contents when you look at the filename cosmo.jpg? If you’ve ever worked with image files, the filename extension (i.e., that sequence of letters and numbers after the final period in the filename) is a great hint about what’s in the file. By convention, the extension .jpg means that the file contains an image encoded in the JPEG standard.[5]
Our computers have been programmed to do the same thing. When we double-click a file like cosmo.jpg, our computers look at the filename extension and guess that they should load the file into a program that can display JPEG images.
While this is normally what we want to happen, this outcome (i.e., a window containing an image) is the result of a program interpreting the contents of the image file. It doesn’t tell us what is actually stored in that file.
Let’s try removing the hint and see what our computer does. In other words, make a copy of cosmo.jpg and name the copy cosmo. Now our computer can’t use the file extension as a hint to determine what to do when opening the file. Next, let’s ask Microsoft Visual Studio Code (VS Code) to display the file cosmo.[6] When we double-click the file cosmo, VS Code shows an alert that tells us, “The file is not displayed in the editor because it is either binary or uses an unsupported text encoding. Do you want to open it anyway?” Putting aside what VS Code means by “binary,” we’ve learned about text encodings. Clearly, VS Code peeked inside the file to see if it recognized the file as a text file in one of its known encodings. It didn’t. For fun, let’s see what happens if it tries to interpret cosmo as a text file. Click “open it anyway.”
Yikes, this doesn’t look anything like a text file … because we know it isn’t!
OK, but we don’t want VS Code to use an incorrect interpretation. We want no interpretation. When you say such a thing to computer scientists, they’ll reach for their favorite “hexdump” program. There’s one with that name on most Unix-based systems, and there’s an extension for VS Code that does that same work. Let’s use it now.
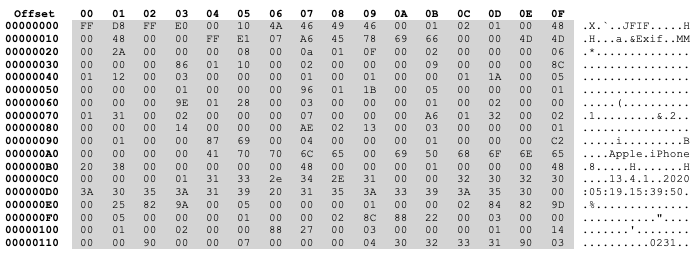
Fig. 13 The start of the raw data in cosmo.jpg, as displayed by a hexdump program.#
Reading a hexdump. Figure 13 shows the output of hexdump when it reads the file cosmo.jpg. The pairs of characters in the shaded two-dimensional (2D) array in the middle of this figure are hexadecimal numbers corresponding to the contents of the file. Yes, the file contains nothing but lots and lots of numbers.
The eight-digit numbers at the left and two-digit numbers along the top (both also in hexadecimal) exist to make it straightforward for you to determine the index of any pair of digits in the central shaded box, when you think about the contents as a long one-dimensional (1D) sequence of pairs. For example, the first pair of hexadecimal digits in the upper left-hand shaded corner is FF, and this pair is given offset 00000000 (i.e., the row number plus the column number). The next pair to the right (D8) is given the offset 00000001. The last pair in the first row (48) has offset 0000000f, and it is followed in the file by the first pair in the second row (00) at offset 00000010. In other words, while hexdump prints the file contents as a 2D array, you should think of it as a long 1D array.
Finally, the characters to the right of the shaded box in Figure 13 are an ASCII interpretation of each pair in the shaded box. For instance, 4A at offset 00000006 is the letter capital-J in the ASCII text encoding.
We can see that this isn’t a normal text file, since most of the ASCII interpretations are the period character (.), which means that a pair is either: (1) really the ASCII encoding for the period character; (2) the ASCII encoding for a space character that hexdump prints as a period character; or (3) a numeric value not corresponding to any displayable ASCII character. The last case could, for example, be the ASCII value for the newline character, which we’ve expressed as \n in our scripts.
You Try It
Figure 13 illustrates that some pieces of our image file are actual ASCII strings. For example, you can see the string 'Apple iPhone' starting at offset 000000a4. Many file formats are structured like the messages we passed between processes in one of Chapter 5’s exercises: they include a header with extra information (called metadata) about the main content. In the JPEG file format, this header can include information such as the type of device that took the image. Or consider another piece of metadata. In Figure 13, can you find the offset for the date and time on which the picture was taken, as stored in the header?[7]
Hexadecimal explained. I’ve mentioned hexadecimal numbers several times over the last few chapters, and now is a good time to make sure we are all comfortable with what this exactly means.
Look at the top row of the hexdump in Figure 13. The first pair (i.e., the label on the leftmost column of the shaded 2D array) is 00 and the rightmost one 0F. Now count the number of columns. I’ll wait.
You should have counted to 16. A hexadecimal number system is one that contains 16 symbols that correspond to the 16 symbols in the right-hand digit of these 16 pairs.
You’ll notice that the first ten of these symbols are the same ones we use every day in the decimal number system: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. The ordering here is significant in computer science for two reasons. First, you’ll often hear that computer scientists start counting from 0 (called zero-based numbering) because they often think in terms of an index in a sequence. We learned that we access the first element of a Python sequence with the index 0, and this zero-based numbering hints at the representation of the actual sequence in the computer’s memory. In sequences (e.g., a Python string), the first element is stored at the start of the string’s storage (i.e., at offset 0 of the storage that holds the string). Similarly, the first hexadecimal pair in our hexdump is at offset 0.
The second reason is simpler. Zero is a great place to start in counting if you realize that what comes before one of something is none of that thing! When we want to count something in code, we’ll want to initialize our counting variable to 0. If you don’t, you’ll be adding 1 to an unknown value in your counting variable!
Back to hexadecimal. “Hexa-” is a combining form that means six, and so you can think of hexadecimal as a number system with “six more things than ten.” What symbols are used for these six extra things? Well, we have run out of single digits, and so convention has us use the first six letters of the English alphabet: A, B, C, D, E, F.[8]
Our hexdump illustrates this way of counting in action. The first item in the hexdump sequence is FF and is accessed with the index 0. The second is D8 and is accessed with the index 1. Those indices are the same in both decimal and hexadecimal, and they continue to be the same up through index 9 (the second instance of the item with value 46). How we write the next index after 9 depends on which base we’re using to count. Decimal is a base-10 system (i.e., it uses 10 symbols), while hexadecimal is a base-16 system (i.e., it uses 16 symbols). As such, the next item in the hexdump (i.e., the second 00 in the first shaded row) is index 10 in base-10 and A in base-16. The first item in the second row of the hexdump (00 again) is index 16 in base-10 and 10 in base-16, and so forth.
Tip
The way that the 1D sequence is laid out in the displayed 2D array makes it so that adding a row’s offset value to a column’s offset value never requires you to do a carry. In fact, the last digit of the column’s offset value just replaces the final zero of the row’s offset value!
You may have learned that 10 in base-10 represents \(1*10^1 + 0*10^0\) where each digit gets multiplied by the base raised to the position of that digit counting from the right (and starting with 0).
Knowing this, what then do you think 10 is in base-16? Using the approach that helped us understand base-10, it would be \(1*16^1 + 0*16^0 = 16_{10}\). We place a subscript-10 on the 16 to remind us that we’re now back in base-10.
You Try It
What is the index, in hexadecimal, for the first occurrence of the value 1B in the hexdump of cosmo.jpg? What is the decimal value of that index?[9]
Converting between number systems. You should take the time to completely understand how to convert back and forth between base-10 and base-16 representations. If you have any questions at this point, there are many resources online that can help. But once you understand how to do this work, you can use the Python interpreter to do the grunt work of converting numbers between different bases. Remember that computers are built to do numerical work!
To convert a number in another base, like 16, to decimal, you simply need to evaluate int('11e', base=16), where '11e' is replaced by the number you want converted. Notice that the hexadecimal number is specified as a string.
int('11e', base=16)
If you want to know the hexadecimal value of a decimal number—say 286—you execute hex(286), where hex is a Python built-in function that takes a single integer argument.
hex(286)
When you run the hex command, you’ll see that the Python interpreter prepended the string '0x' to the hexadecimal equivalent of 286. This prefix is how you and the interpreter know that the string represents a number in base-16, not base-10.
Does the computer see my dog? While we can see that the bunch of numbers saved in cosmo.jpg and then displayed as an image contains a dog, can the computer recognize that there’s a dog in this sea of numbers? The short answer is yes—with the help of machine learning (ML), which we will discuss in Chapter 17. If you have a phone that unlocks with facial recognition, you’re already using this technology in your daily life. For now, we can get an idea of how this works and, importantly, learn that the work going on in the bowels of our computers is really nothing more than math on numbers.
To work with images, we are going to use the Python Imaging Library (PIL).[10] This very handy library includes support for a wide range of file formats, including JPEG, and it allows us to write only a few lines of code to perform an extensive set of image-processing tasks.
For example, similar to what we did when we read the text files containing the story of The Cat in the Hat, we will use the Image.open method to read the image data into an Image object, which I’ve named im in edges.py. After processing this image, our scripts will write out the new image to a file called out.png using the Image.save method. Feel free to change the filename and file extension; the extension tells the PIL what format to use when saving it. To see the resulting image, simply open the saved file as you would with any image file (e.g., double-click the file).
1### chap06/edges.py
2from PIL import Image, ImageFilter
3
4imfile = input('Name of imagefile: ')
5
6with Image.open('images/' + imfile) as im:
7 # Apply a filter that detects edges
8 filtered = im.filter(ImageFilter.CONTOUR)
9 filtered.save('images/out.png')
Image objects have many methods. To highlight the edges, or contours, of the things in an image, we apply a convolution filter.[11]
You Try It
Run edges.py and input cosmo.jpg. After the script has run, in out.png, you’ll see that the application of this filter (i.e., a mathematical transform of the numbers in cosmo.jpg) nicely outlines my dog.
Painting a picture. To understand what took place when we ran a convolution filter, we are going to use the PIL to build a very simple image that contains a single edge and then write a few lines of Python code to detect that edge. The script edge1.py gets us started.
1### chap06/edge1.py
2from PIL import Image
3
4# Width and height of our image
5sz = (100, 100)
6
7# Create a single plane of grayscale pixels, initialized to black
8im = Image.new('L', sz)
9
10# Create direct access to the pixels in the image
11pixels = im.load()
12
13# Set the color of each pixel
14for i in range(sz[0]):
15 for j in range(sz[1]):
16 # Creates a diagonal fade
17 pixels[i,j] = i + j
18
19im.save('images/out.png')
This script begins by creating a new Image object that contains a 2D array of size 100×100, as specified by the second parameter to the Image.new call.[12] This 2D array is the canvas on which we’ll paint our image. However, unlike a picture that we create with a paintbrush, the picture we will build is more like one from a paint-by-number kit, where each element in this 2D array is of a fixed size and painted with a single color. Every picture we take with a digital camera is created in this way, and each element in the 2D array that comprises a digital picture is called a pixel, which is short for picture element.
Pixels come in different ranges of colors. Our script asked the Image module for pixels that can be colored with one of 256 different shades of gray, where 0 represents pure black and 255 pure white. It specified this grayscale coloring by passing the string value 'L' as the first parameter to the Image.new call on line 8. This parameter is called the mode, and in an exercise, you will change the mode to 'RGB' so that you can build pictures with a rainbow of colors. In RGB mode, the number 0 still represents pure black, but we now have more than 16.7 million colors between the color black and the color white (16,777,216 colors in total to be exact). As a last example, we might have specified the mode '1', which encodes pure black as the number 0 and pure white as the number 1. In this mode, you have only two colors in your palette.[13]
Bits. Each of these modes has two things in common: 0 represents black; and the total number of colors between black and white, inclusive, is a power of 2. The encoding for white, then, is \(2^{numberOfEncodingBits} - 1\) in each of these modes.
A bit is the most elemental unit of storage in our computing systems. It represents a single digit in the base-2 numbering system, also called binary numbers. With a single bit, the value of this binary number is either 0 or 1. The value 2 (base-10) is encoded as 10 (base-2), following the same reasoning we used when we discussed base-10 and base-16 numbering. As an illustration, Figure 14 counts from 0 to 19 in each of the bases 10, 2, and 16.
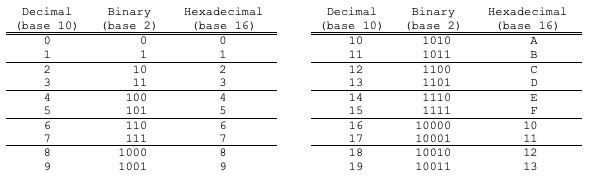
Fig. 14 A listing of how the numbers from 0 to 19 are written in the bases commonly used in computing. Notice that a new digit is added when the count equals the base.#
Great, but you might be wondering why computers use binary numbering. You might claim that hexdump didn’t display the numbers contained in my JPEG file in base-2. Yes, that’s true about hexdump, but this was a usability design decision that the creators of hexdump made.
To understand this design decision, answer the following question: For which of the following pairs of numbers is it easier for you, a human, to tell that the two values in the pair are not the same: 11011000 and 11011100, or D8 and DA? I’ll guess that you’ll say the latter, and this difference in ability only increases as the number of digits you’re scanning increases.
Hexdump uses base-16 because it is easier to read hex numbers and a straightforward process to convert back and forth between base-2 and base-16. Starting from the right-hand end of a base-2 number, you group together the rightmost 4 bits and convert them into a single hexadecimal digit. You then grab the next 4 bits and repeat until you run out of bits. For example, 11011000 becomes 1101 1000, which becomes D 8, which we can push back together as D8. (Feel free to run the process in reverse, when needed.) When you understand this, I hope you realize that hexdump is showing us the bits in the JPEG file.[14]
One finger, no thumb. The careful reader will interrupt at this time and point out that I still haven’t told you why computers store numbers with binary digits and not, say, decimal digits. A simple answer is that humans learned to count using their fingers, and since most of us have 10 fingers, base-10 numbering comes naturally to us. Computers don’t have any fingers, and what is natural for them is sensing the difference between on and off.
If you take a course in digital logic design, you’ll learn that modern computers, and most every piece of logic in them, are built from very simple switches, which are either on or off. Yes, these switches are like the light switches in your home. Flip the switch up and the light goes on; flip it down and the light goes off. From this incredibly simple switch, we can build the large memories and fast processors found in the smartphones we hold in our hands, the laptop computers on our desks, and the corporate servers in the cloud.
The digital abstraction. When we build smartphones, computers, and servers from circuitry that acts like simple switches, we call the result a digital device. This nomenclature reminds us that we are relying on another abstraction boundary: the digital abstraction.
What a digital circuit senses as “on” (or a 1 value) is a real-world value (called an analog or continuous value) somewhere near the ideal “on” value. You can think of this as the rounding we learned in grade school. We might measure some length as 1.03 miles, and we round it to 1 mile when all we care about is roughly how many miles it is from my home to my grandmother’s house. Similarly, a value of 0.042 miles is rounded to 0 miles.
You Try It
How should we treat a measurement of 0.47 miles? Should we treat it as 1 mile or 0 miles? In other words, should we round this value up or down?[15]
The magic of digital circuits is their ability to ignore—and, in fact, avoid accumulating—a certain amount of imprecision away from the ideal values.[16] Because of this magical property of digital circuits, we can pretend, for example, that the file cosmo.jpg in my computer’s memory (or in a solid state drive, or on a magnetic hard drive, or being transmitted across the Internet) is just a bunch of binary numbers, even though the first 1 value in the file is not actually exactly 1 (or the same exact value) on any of those mentioned media.
Bits, bytes, and nibbles. With this new knowledge, let’s return to our edge1.py script. The code creates a 100×100 2D array of pixels, and each pixel can contain one of 256 shades of gray. Since 256 is \(2^8\), this explains why 'L' is described as “8-bit pixels, grayscale” on the documentation page.[17]
Eight bits grouped together occurs so frequently in computer science that this grouping is given its own name: a byte. If you look back at the hexdump, you’ll notice that this is what hexdump is indexing. FF is the value of the first byte in cosmo.jpg; D8 is the value of the second byte.
You might also hear the term nibble, which is half a byte or 4 bits. Half a byte like D8 is simply one of the hexadecimal characters.
You’ll also recognize the term byte from the unit of size in which you buy computer memory or hard-drive storage. My laptop has 16 gigabytes (GB) of memory, where giga- means \(10^9\). In other words, my laptop has a little bit more than 16 billion bytes of memory.[18]
Setting a pixel’s color. By default, Image.new sets each pixel in our created 2D array to the color black. Why black? Because this default is easy. Every mode defines black as 0, and if we fill the 2D array with zeros everywhere, we get a completely black picture.
To make a more interesting image, edge1.py contains a pair of nested for-loops (lines 14−17) that paints each pixel in the Image object’s 2D array of pixels with a color of our choosing. To access the image’s individual pixels, the script calls the Image.load method (line 11), which returns an object that supports the Python indexing syntax (i.e., square brackets).
With this pixels array in hand, the script uses the nested for-loops (lines 14−15) to produce an index i,j, which I’ll write as [i,j], that allows us to set the color of each pixel. The color chosen for each pixel is determined by a simple summation of the two index values.
What kind of picture will this create? The first iteration of the outer loop sets i to 0, and then its body runs the first iteration of the inner loop, which sets j to 0. The inner loop’s body then sets the pixel at [0,0] to the value 0, which is the encoding for the color black.
But which pixel in the 2D pixels array is the pixel at [0,0]? If you read the PIL documentation, it says that [0,0] is defined to be the upper left-hand corner of the image. There’s nothing special about this choice other than that’s how the code in the library has been designed to work.
In Chapter 7, we’ll learn more about how a nested loop structure causes us to move through the pixels in an image. For now, we only care that, as we move right and down in the pixels array, we will store ever larger sums, which in our color palette moves us closer to the color white. So, it sounds like this script will produce an image with a diagonal fade, from black in the upper left-hand corner to white in the lower right-hand corner.
You Try It
Run edge1.py and see that it does produce an image with a diagonal fade.
Saturation. Let’s try making a bigger image using our simple method for creating a diagonal fade. In particular, let’s change the value of sz from (100, 100) to (400, 400) and rerun the script.
1### chap06/edge2.py
2from PIL import Image
3
4# Width and height of our image
5sz = (400, 400)
6
7# Create a single plane of grayscale pixels, initialized to black
8im = Image.new('L', sz)
9
10# Create direct access to the pixels in the image
11pixels = im.load()
12
13# Set the color of each pixel
14for i in range(sz[0]):
15 for j in range(sz[1]):
16 # Creates a diagonal fade
17 pixels[i,j] = i + j
18
19im.save('images/out.png')
Our desired fade appears only in the upper left-hand corner of the generated image. Why do you suppose that is?
Perhaps we can figure it out if we look at the values stored in the pixels array after the work done by the nested for-loop. In particular, let’s print the value of the last pixel in our image, whose value is stored at pixels[399, 399].
print(pixels[399, 399])
Its value is 255. What value did we try to write into that pixel? It should have been 399 + 399 or 798. Why did 798 become 255? In fact, if you look at every pixel beyond the diagonal where i + j becomes equal to 255, you will find that the value of those pixels is 255.
Here’s a hint: What did we say about the pixels in our image when we created the image object? We said that the image would be full of 8-bit pixels. What is the biggest decimal number we can represent with 8 binary bits? Well, what is 11111111 in decimal? Go ahead and ask the Python interpreter to evaluate the following expression:
int('11111111', base=2)
So, what has the assignment done when we asked it to store a number bigger than 255? Right! It simply stored the biggest number it could. This is called saturation. It is equivalent to the functionality of the volume circuitry on your cell phone. You can keep pushing the volume-up button, but eventually the volume hits its maximum value and stays there no matter how many more times you hit the button to increase volume.
What do you think will happen if we try to store -1 in pixels[399, 399]? Right again! No matter how many times you push volume-down, you can’t get your volume to go any lower than 0 or off.
pixels[399, 399] = -1
print(pixels[399, 399])
Putting this all together, we asked the PIL to create an image of 400×400 pixels, where each pixel held an 8-bit value between 0 (black) and 255 (white). It (silently) made sure that the image’s pixel array never contained any values outside this range. When we tried to store a value greater than 255 or less than 0, it “saturated” that value at either 0 or 255.
Overflow and Underflow. Many programming languages allow you to define a variable and specify that it can contain only integer values between 0 and 255. A computer scientist would say that such a variable has the type unsigned byte. The word “byte” indicates that we need only 8 bits to represent every possible unique value, and the word “unsigned” means that the values should be interpreted as all greater than or equal to zero. This exactly describes the encoding we use for 8-bit, grayscale pixels.
We will learn more about the benefits of types later. For now, I want to introduce you to the ways that different programming languages might handle an operation that produces a value that doesn’t fit into an unsigned byte.
Take, for example, the situation with which we’ve been dealing: the addition of two 8-bit, grayscale pixels. As we’ve learned, this addition might produce a value greater than 255, for which we have no 8-bit representation. In general, computer scientists say that the addition overflowed its representation (or just overflowed, for short). Similarly, a subtraction may underflow by producing a value less than the smallest allowed representation. Saturation is one way of “correcting” these situations. In our current problem-to-be-solved, it is a sensible solution because we’re working with image pixels, and there’s nothing blacker than black or whiter than white.
More generally, a running program may not know that a variable represents an 8-bit, grayscale pixel, but only that the variable’s physical representation is an unsigned byte. In this case, saturation may not be the right action to take. Instead, a better action might be to raise an exception.
We’ve seen several types of exceptions, and they are ways for a running program to indicate that something happened that it doesn’t know how to handle. If your script doesn’t register a way to handle an exceptional event, the event will terminate the running instance of your script.
Sometimes, the designer of a programming language will choose to ignore particular kinds of overflow and underflow. For example, addition on unsigned integers in the C programming language never, by definition, overflows. If you add two unsigned, 8-bit numbers in C, the result is the sum of the two numbers modulo 256. In other words, unsigned addition in C is like adding on an analog clockface: when you add one to the biggest number on the clock face, you find yourself at the smallest number on the clockface. Another way to think about C’s unsigned add is that you perform the addition and then lop off the most significant bits that don’t fit in the physical representation. All are just different ways of describing the concept of modular arithmetic.
Finding edges. We are finally ready to build a picture containing an edge and then do some simple math to highlight that edge’s location in the image.
The script edge3.py builds two images. In the first (called im), it sets the color of all columns in the image array with indices below 25 to black and the rest to white, which creates a vertical boundary between the black and white areas. The second image (called filtered) computes each of its pixel values by performing some math using a selected group of the pixels in im, as I’ll explain in detail in a moment.
1### chap06/edge3.py
2from PIL import Image
3
4# Width and height of our image
5sz = (100, 100)
6
7# Create a single plane of grayscale pixels, initialized to black.
8im = Image.new('L', sz)
9
10# Create direct access to the pixels in the image
11pixels = im.load()
12
13# Set the color of each pixel
14for i in range(sz[0]):
15 for j in range(sz[1]):
16 pixels[i,j] = 0 if i < 25 else 255 # vertical boundary
17 # pixels[i,j] = 0 if j < 25 else 255 # horizontal boundary
18
19# Save initial image
20filtered.save('images/out_orig.png')
21
22# Create a new B&W image into which we'll put the filtered result
23filtered = Image.new('L', sz)
24fpixels = filtered.load()
25
26# Apply an edge-detection convolution (it's just math for B&W only!)
27for i in range(1, sz[0]-1):
28 for j in range(1, sz[1]-1):
29 fpixels[i,j] = (pixels[i-1,j-1] * -1 + pixels[i-1,j ] * -1 +
30 pixels[i-1,j+1] * -1 + pixels[i ,j-1] * -1 +
31 pixels[i ,j ] * 8 +
32 pixels[i ,j+1] * -1 + pixels[i+1,j-1] * -1 +
33 pixels[i+1,j ] * -1 + pixels[i+1,j+1] * -1)
34
35# Save resulting image
36filtered.save('images/out_filtered.png')
The script creates the first image using the syntax for Python’s conditional-assignment statement (line 16). The statement might look intimidating at first, but you’ll get it if you take the statement a piece at a time: pixels[i,j] is set to the value 0 if the condition is True; otherwise, it is set to 255. The condition in the statement is i < 25, but it could be anything that evaluates to True or False.
After saving this initial image im, the script then creates an entirely black filtered image of the same size as im. The interesting work is in the body of the second nested for-loops, which you can think about as a computation that uses a sliding window with nine panes of glass organized as three rows of three columns. The script centers this 3×3 window over a [i,j] pixel in im and uses the values of the window’s pixels to compute the color of the [i,j] pixel in filtered.[19]
Figure 15 illustrates the work of this second pair of nested for-loops (lines 27−33). The pixels image in the figure is like our script’s im image except that we switch from black to white after three columns (not 25). The fpixels image is the result of the fpixels computation on lines 29−33 for each [i,j] pixel. I’ve drawn the 3×3 sliding window over a pixel [i,j] and shown the computation that takes place. This computation produces a value of −765, which is saturated to 0 (black).[20]

Fig. 15 An illustration of the sliding window computation in edge3.py that highlights the boundaries of an object (like a dog) in a digital image.#
Now think about this computation when every pixel in the 3×3 sliding window is the same color: the heavy weighting on the [i,j] pixel exactly cancels the summed weighting of the surrounding 8 pixels. The computed value is 0, and the [i,j] pixel in the filtered image is painted black.
However, when the leftmost column of the sliding window of pixels is black and the rightmost two columns are white (i.e., slide the window in Figure 15 one column to the right), the computation produces the value (8 * 255) − (5 * 255) = 765. Of course, saturation occurs, and the pixel is painted with the value 225 (white).
You Try It
Run edge3.py, and you’ll see that the filtered image contains a white line where the edge between the black and white regions were in the original image—like the fpixels image in Figure 15. Comment line 16 and uncomment line 17 to switch from a vertical to a horizontal edge; the computation handles a boundary of any orientation.
You have now done all that the ImageFilter library did when our code in edges.py applied a CONTOUR filter. In this way, a computer can highlight the dog-shaped blob in cosmo.jpg. Knowing that the blob looks like a dog requires machine learning, a topic for later.
