Chapter 12: Divide and Conquer

The last chapter ended with a suggestion that we add a heuristic into our goal-directed search algorithm. Without a heuristic, every item on the frontier appears equally good. But with one, our search algorithm explores first the frontier list’s potentially most fruitful item. You can think of the heuristic calculation as solving a simple version of the problem (e.g., which direction would a crow fly to get to our driving goal). While not guaranteed to lead to an optimal solution, good heuristics are fast to compute and likely to prioritize the right frontier items, which can get the search algorithm to a near-optimal solution quickly.

But finding the highest priority item in a list is another kind of search problem. We don’t want to replace the simplicity of an uninformed search (i.e., the appending and popping of items from the ends of the frontier list) with an expensive search of this list, which might make an informed search slower than an uninformed one. To avoid this, informed searches keep the frontier list ordered by priority. And creating such an order is the job of a sorting algorithm.

Sorting appears as a part of many algorithms in computer science, and it makes many of the problems we want solved more efficient and the answers we get more useful. For example, Google sorts its search results before presenting them to the user, since users expect to see the most relevant results at the top of the returned list. In performing this sort, several heuristics are used to assign a score to each returned result (e.g., a person in a particular geographic location probably desires results in that geographic location more than other locations). To similarly aid us in quickly finding that which we care about, the words in a book index are sorted alphabetically.

You Try It

Think about your daily life and identify three or four other examples of places where things are sorted for your convenience.

Because of the importance of sorting, it’s another well-studied computational problem. While modern programming languages provide useful sorting primitives—and we’ll cover those found in Python—the first third of this chapter goes from a formal specification for sorting to two algorithms with different computational complexities that satisfy this specification. The more computationally efficient of these introduces a new problem-solving technique, called divide and conquer. It works well when a problem can be divided into smaller, similarly structured problems. Sorting is exactly such a problem, and we’ll see how to sort a list of numbers by organizing it as one in which we separately sort the list’s two halves and then quickly combine the sorted results.[1]

The implementation of this more computationally efficient sorting algorithm also introduces you to a new coding technique called recursion, which is the more natural way to write divide-and-conquer algorithms. You’ll learn to write recursive functions from a recursive specification in the middle third of this chapter.

The chapter’s last third pulls all these ideas together by illustrating how to design a recursive solution to a problem that may not initially appear amenable to a divide-and-conquer approach. This is not easy and takes significant practice, but the simplicity of the solution script is the reward for the hard work.

Learning Outcomes

Learn about divide-and-conquer as a problem-solving technique and recursion as a method for writing such algorithms. Sorting, which can be solved using divide-and-conquer, is a tool we often use (e.g., in our solutions to search). You will code two very different sorting algorithms and learn about Python’s built-in mechanisms for sorting. Because our normal looping mechanisms are not a great way to code divide-and-conquer algorithms, you’ll learn to write recursive functions. Finally, given a problem that at first doesn’t seem amenable to a divide-and-conquer technique, you’ll marvel at the conciseness of recursion to express a solution to this problem. After completing this chapter, you will be able to:

• Write a broadly applicable specification for sorting and understand how to extend this specification to cover a wide range of sorting problems [design and CS concepts];

• Use the sort method on Python lists and the sorted built-in function to solve a wide range of sorting problems [programming skills];

• Pass a function as a parameter so that you can specialize the behavior of Python’s sorting functions [programming skills];

• Describe and code a brute-force sorting algorithm called insertion sort, which is probably what you use when sorting the cards you’ve been dealt [CS concepts];

• Understand how splitting work can lead to an efficient solution and code an example of this using binary search [design and CS concepts];

• Employ a divide-and-conquer approach to create a more efficient sorting algorithm called merge sort [design and CS concepts];

• Code merge sort in iterative and recursive styles [CS concepts and programming skills];

• Describe the key components of a recursive function [design and CS concepts];

• Search for patterns in your problem to see if it might be amenable to a divide-and-conquer approach and recognize the base cases in a recursive implementation [design].

A specification for sorting. We’ve talked about the importance of sorting and now let’s understand how to create a sorted list from an unsorted one. We begin with a formal specification for sorting:[2] Given a sequence of \(n\) numbers, \([a1, a2, ..., an]\), produce an output sequence \([a1', a2', ..., an']\) such that \(a1' <= a2' <= ... <= an'\).

Does this definition match your intuitive understanding of sorting? If you think about a list of numbers and a desire to reorder these numbers so that the smallest is first in the output list, it probably does.

But what if you wanted to sort the list with the largest number first? The definition still works if we consider \(<=\) to be an ordering operation that we specify and not the less-than-or-equal-to operator. In this way, we can sort a list of numbers or strings in either ascending or descending order simply by providing the ordering operation we want applied (i.e., the formal specification now begins: Given a sequence of \(n\) numbers and an ordering operation \(<=\), produce …).

But still, does this updated definition cover everything you’ve ever sorted? What about when faculty sort their students by full name? How about when you sort your family from shortest to tallest for the annual family picture? We know that faculty sort students initially by last name and then, if needed, by first, and while our family members aren’t numbers, height is a characteristic we can use to order them. Neither of these “complications” fundamentally changes the work we do to sort. They simply specify the work to be done by the ordering operation or the attribute of the objects we’ll used to sort them.

Hopefully, you agree with me that this extremely short definition does an excellent job of capturing the essence of sorting, even if we might want to adapt it to specify exactly how we’d like the sorting comparison done.

Sorting in Python. As an example of how programming languages handle this generalization, consider the two functions built into Python:[3]

• The list class contains a sort method that sorts a list object in place, which means that the original contents of the list are replaced with the sorted contents.

• The built-in function sorted takes an object of an iterable type (e.g., a sequence or a dictionary) and returns a new sorted list. The original object is left unchanged.

Let’s build ourselves a few unsorted lists so that we can play with these functions. We’ll use the lists a, c, and w below throughout the rest of this chapter.

### chap12/unsort.py

# Some unsorted lists to use as examples and tests
def unsort():
    a = [5, 2, 1, 4, 7, 3, 6]
    c = ['6\u2663', '3\u2663', '2\u2660', '2\u2661', '4\u2663', '6\u2662', '5\u2660']
    w = ['The', 'sun', 'did', 'not', 'shine',
        'It', 'was', 'too', 'wet', 'to', 'play']
    return a, c, w

Often you can use Python’s two sorting functions without any parameters, as illustrated in the next two code blocks.

### chap12/sorting.py

print('The `sort` method on Python lists sorts in-place')
a, c, w = unsort()
a.sort()
c.sort()
w.sort()
print(f'a = {a}\nc = {c}\nw = {w}\n')

### chap12/sorting.py

print('The `sorted` built-in function leaves the input object unchanged')
a, c, w = unsort()
aa = sorted(a)
cc = sorted(c)
ww = sorted(w)
print(f'aa = {aa}\ncc = {cc}\nww = {ww}\n')

You Try It

Run the code above and think about how Python sorts integers and strings. The integers in list a were clearly ordered from smallest to largest. The list w contains words as strings, and what do you notice about the sorted result? What does that tell you about how Python sorts letters? The list c contains seven cards from a typical card deck expressed as strings, and the unicode values in each string are playing card suit emojis. How does Python sort unicode values?[4]

Looking back to Chapter 10, where we built a book index, you’ll see that we used the built-in sorted function; with it, we sorted our dictionary of word-reference pairs. Python dictionaries are iterable objects, and calling sorted with a dictionary returns a sorted list of the dictionary’s keys, which was exactly what we wanted to print (see lines 63-66 in chap10/index32.py).

These examples work because: (1) the way we wanted to sort the list elements and dictionary keys matched these functions’ default action (i.e., sort with the “smallest” item first); and (2) the classes for these iterable objects implement the magic method __lt__, which sort and sorted use behind the scenes to determine the sorted order.

Sorting in descending order. But what if we wanted to sort so that the “largest” item came first? Both sort and sorted support this behavior through the setting of the named parameter reverse. It is False by default, but by setting it True, the sort is “reversed” from its default. Let’s reverse-sort our example lists to see this in action.

### chap12/sorting.py

print('The `sort` method reversed')
a, c, w = unsort()
a.sort(reverse=True)
c.sort(reverse=True)
w.sort(reverse=True)
print(f'a = {a}\nc = {c}\nw = {w}\n')

print('The `sorted` built-in function reversed')
a, c, w = unsort()
aa = sorted(a, reverse=True)
cc = sorted(c, reverse=True)
ww = sorted(w, reverse=True)
print(f'aa = {aa}\ncc = {cc}\nww = {ww}\n')

Sorting with your own comparison function. But we also talked about more “complicated” sortings that professors do with student names and you do with your relatives for a family picture. The two Python sorting functions handle this type of complicated data through their key parameter. It allows you to do things like: (1) sort a list of words without worrying about the capitalization of the words; and (2) sort a list of complex objects using only one or a few of the objects’ attributes.

The key parameter takes a function. We know how to define a function and how to call a function, but what does it mean to say that a parameter takes a function? Well, a function is just another Python object, and instead of invoking that function using its name and a pair of parentheses (e.g., str.lower()), we can assign a new name to that function by referring to its current name (e.g., also_lower = str.lower). That’s all that occurs when we pass a function as a parameter (i.e., give the function a new name). So, to sort our unsorted list of words without worrying about each word’s capitalization, we simply write:

### chap12/sorting.py

print('`sort` ignoring capitalization')
a, c, w = unsort()
w_caps = sorted(w)
w_nocaps = sorted(w, key=str.lower)
print(f'w_caps = {w_caps}')
print(f'w_nocaps = {w_nocaps}')

Inside the implementation of sort, str.lower is applied to each item in the input list (i.e., w) and the result of str.lower is the value used in the comparison to determine whether this item comes before or after another item.

But we don’t have to set the parameter key to the name of a function that someone else wrote. We can pass the name of a function we’ve written! This will allow us to sort a list of complex objects using only one or a few of the objects’ attributes.

For instance, imagine we have a database of records, where a record is a block of information consisting of many attributes. We’ll build an example of such a database as a simple list, and each list item will be a tuple. The list items are our database records, and the tuple items the values for each record field. Here’s an example of such a database using a set of characteristics about the individuals that were involved in the first class I taught using this book:

### chap12/sorting.py

cs32_staff = [
    # fields: name, fav_color, fav_animal, batting_avg
    ('Mike', 'blue', 'dog', 0.042),
    ('Dhilan', 'brown', 'lion', 0.333),
    ('Manana', 'black', 'golden eagle', 0.395),
    ('Emily', 'forest green', 'bird', 0.400),
    ('Jiahui', 'red', 'bear', 0.392),
    ('Matthew', 'yellow', 'ram', 0.299),
    ('Karly', 'white', 'dolphin', 0.315),
    ('Sid', 'baby blue', 'orange', 0.215),
    ('Nadine', 'purple', 'owl', 0.357),
    ('Patrick', 'green', 'dragon', 0.278),
    ('Cosmo', 'yellow', 'squirrel', 0.043),
]

To sort this list by batting average, we define a function that takes a tuple as found in this database and returns the value of the tuple’s fourth field. We then set the key parameter to the name of this function, and since we want the individuals with the biggest batting average first, we also set reverse to True.

### chap12/sorting.py

def batting_avg(t):
    return t[3]

print('`sorted` using an attribute')
print(sorted(cs32_staff, key=batting_avg, reverse=True))

Sorting problem solved!

You Try It

Your key function doesn’t just have to use the value of a single attribute; it can combine the values of several attributes or pieces of these attributes. Can you figure out the function you’d write to sort a list of names by last name and break ties by first name? Try your solution on this list of names: ['Ada Lovelace', 'Grace Hopper', 'danah boyd', 'Moses Liskov', 'Barbara Liskov', 'Anita Borg']. Be careful with capitalization! You can find an answer in chap12/sorting_names.py.

Sorting playing cards. Let’s return to our initial specification and look at two different algorithms for sorting. We’ll begin with the brute-force method many use to sort the hand dealt to us when playing a card game (assuming that the game allows and benefits from having a sorted hand). Here’s an algorithmic description (i.e., pseudocode) of this method:

1. You pick up the unsorted stack of cards and fan them out in your hand. Let’s assume you want the smallest numbered cards on the left and the face cards and aces on the right.

2. You begin by looking at the two leftmost cards and ask yourself: “Are these two cards in the right order?” If not, you swap them.

3. With these two cards in sorted order, you now look at the 3rd card in your hand, and you ask yourself: “Where does this card belong in the sorted list of first two cards?” If it needs to go somewhere other than where it is (i.e., last in the sorted sequence), you pull it out and insert it where it belongs.

4. With these three cards in sorted order, you now look at the 4th card in your hand, and you ask yourself: “Where does it belong in the sorted list?” And so forth.

Do you see the pattern? Computer scientists call this algorithm an insertion sort, and we can code it by recognizing that it involves a pair of nested for-loops. The outer loop visits each card in the unsorted part of our hand; it corresponds to the numbered steps in the pseudocode above. We need an inner loop to implement the act of insertion in each numbered step because it’s not easy to insert an element where it belongs in a sorted list. To do this, our code will walk down the sorted part of the list swapping the unsorted item with the sorted item before it until it reaches the position where it belongs in the sorted order.

You Try It

This description might be hard to follow. Look at insertion_sort in the code block below, and then run it with the three observe functions uncommented (on lines 12, 18, and 23). If you study what the routine prints for each iteration of the for-loops, you’ll better understand its operation.

### chap12/insertion_sort.py

def insertion_sort(s):
    """Sorts the unsorted sequence s in place"""
    for i in range(1, len(s)):
        # observe_start(s, i)

        for j in range(i, 0, -1):
            if s[j-1] > s[j]:
                # Swap the two items
                s[j-1], s[j] = s[j], s[j-1]
                # observe_swap(s, i, j)
            else:
                # When swaps are done, the ith element is where it belongs
                break

        # observe_done(s, i)

### chap12/insertion_sort.py

a, c, w = unsort()

print(f'Sorting list A: {a}')
insertion_sort(a)
print(f'Sorting list C: {c}')
insertion_sort(c)
print(f'Sorting list W: {w}')
insertion_sort(w)

print(f'Sorted lists:')
print(f'A = {a}\nC = {c}\nW = {w}')

Time complexity of brute-force sorting. Given that insertion_sort contains two nested for-loops that iterate at most \(n\)-times, where \(n\) is the length of the input list, we can surmise that the computational complexity of this approach is \(O(n^2)\). And if you think about the worst-case number of swaps that will occur during an insertion sort, you’ll calculate it to be \((n * (n - 1))/2\).

You Try It

Can you create an input list b of length 5 containing nothing but integers that exhibits this number of swaps (i.e., \((5 * 4)/2 = 10\) swaps)? Leave the observe functions uncommented in insertion_sort so that you can count the number of swaps performed.[5]

I called insertion sort a brute-force approach, and if the computational complexity of this approach is \(O(n^2)\), then there must be a sorting algorithm that does better than this. In fact, there are several[6] but we’ll look at just one. This one works by thoughtfully splitting the problem into two smaller problems.

Binary search. To see why splitting a problem into several smaller instances might help, let’s try this with searching. Recall the guess-the-number script from Chapter 5, and think about the strategy you employ when you try to minimize your number of guesses.

Does this strategy have you guess the numbers in increasing order from the smallest possible number? Of course not. That approach doesn’t use to your advantage the hints given by the computer after each guess. Guessing first the number 1 in the range 1 to 100 means that the computer will respond with “Too small!” when 1 isn’t the hidden number. You could then guess 2, and unless you’re very lucky, the computer’s answer is the same. Continue in this fashion and you never take advantage of the other possible response: “Too big!”

Now consider what happens when your guess leaves unguessed numbers above and below it. Again, assuming that whatever number you guessed wasn’t the secret, the computer’s answer of “Too small!” eliminates more than just the guessed number; it eliminates all the unguessed numbers below it. If you make wise choices, your guesses can eliminate large portions of the search space and quickly get you to the secret number.

The optimal strategy is called a binary search, in which you guess a number at the mid-point of the search space. It’s optimal because an answer of “Too small!” or “Too big!” then eliminates one half of the remaining search space, which is the best you can do on average.[7]

A binary-search algorithm has you continue in this manner (i.e., choosing the mid-point of the remaining search space each time) until you hit the hidden number. In the worst case, it takes at most \(log_2(n)\) guesses to find the hidden number, where \(n\) is the size of the search space.

The guesses function in the next code block implements the binary-search algorithm in a game that has the computer can guess your secret number. This game reverses the participants’ roles in the guess-the-number game we built in Chapter 5. There’s no new Python syntax or operators in this code, but take a few moments to read through it and make sure you understand how it implements binary search.

### chap12/guesses.py

# Global constants for guessing range
LO = 1
HI = 10000

def guesses():
    print("## Welcome to I'LL GUESS YOUR NUMBER ##")
    
    print(f"Please think of a number between {LO} and {HI}, but don't tell me.")
    input("Hit return when you're ready ...")
    
    # Possible user answers
    answers = ['too low', 'too high', 'yes']
    
    # Initializations
    lo = LO
    hi = HI
    
    # Use binary search as the algorithm we play by
    while True:
        # Generate new guess at mid-point
        mid = lo + (hi - lo) // 2
        
        # Grab answer from the player
        while True:
            ans = input(f'Is it {mid}? ').lower()
            if ans in answers:
                break
            print('Please answer "too low", "too high", or "yes".')
        
        # Update range of possible guesses
        if ans == 'yes':
            print('\U0001f60e')
            return
        if ans == 'too low':
            lo = mid + 1
        else:
            hi = mid - 1

You Try It

Run guess.py from the chap12 code repository, which implements guess32.py from Chapter 5 with the same LO-HI range as guesses.py. Using the same secret number that the computer chose, then run guesses.py and see if the computer guesses this secret number in fewer turns. Next, progressively increase HI by a factor of 10 and watch how slowly the number of guesses taken by the computer grows. That’s the power of \(log_2(n)\) growth.

Divide and conquer. This idea of splitting a problem in half to make it easier is at the heart of this chapter’s new problem-solving technique, called divide-and-conquer. And just as we did in a binary-search algorithm, we’ll repeatedly split each smaller problem until we get to a situation where splits are no longer necessary.

To understand this in detail, let’s return to the context of sorting. Given an unsorted list, divide-and-conquer has us split this list in half. This split produces two lists, which most likely are themselves unsorted, but let’s pause and consider what we’d do if the split happens to produce two sorted lists. To be clear, splits don’t sort. But we might be lucky and start with an unsorted list like [1, 3, 5, 2, 4, 6], and when we split this list in half (i.e., between 5 and 2), we’re left with two sorted lists. That’s close to what we want (i.e., a list with all the original elements sorted), and so let’s now ask, given two sorted lists, how would we combine them into a single sorted one?

A function that quickly merges two sorted lists into a single sorted list is not hard to build if we recognize that one of the two first items in the sorted lists must be the first item in the fully sorted list. Let’s take the smaller of the two from its sorted list and append it to an output list. One of the two sorted lists is now one element shorter, but this situation is not any different than the one we just had. We again want to ask: Which of the two items at the front of the two sorted lists should be appended to the single sorted list? We continue like this until we have moved all the items from the two small sorted input lists into the single sorted output list.

That’s the core of the merge function that will combine all the lists we produce through splitting. In other words, we’ll switch from splitting to merging when we recognize that we’ve done enough splitting to produce nothing but sorted lists.

Tip

In general, every divide-and-conquer algorithm has some sort of splitting phase and a complementary merging phase.

The next code block lists an implementation of merge for a divide-and-conquer sorting algorithm. This function takes two sorted lists as input and returns a single sorted list containing all the elements of both input lists. The code is more complex than what I described earlier because it handles the corner cases I glossed over. For example, what do you do if one of the input lists is empty? Lines 6-10 check for this condition and have merge return the other list. Similarly, what do you do in the loop starting on line 18 when you’ve popped all the items off one list and the other isn’t empty? Lines 19-22 check for this condition and have merge append whatever is at the head of the non-empty list.

### chap12/merge.py

def merge(a, b):
    """Given two sorted lists, return a single sorted list"""
    
    # Check for and handle trivial merge cases
    if len(a) == 0:
        return b
    if len(b) == 0:
        return a
    
    # Create a place to put the merged lists
    merged = []
    # Calculate how long the merged list should be
    tot_length = len(a) + len(b)
    
    # Merge a and b
    while (len(merged) < tot_length):
        if len(a) == 0:
            merged.append(b.pop(0))
        elif len(b) == 0:
            merged.append(a.pop(0))
        elif a[0] < b[0]:
            merged.append(a.pop(0))
        else:
            merged.append(b.pop(0))
    
    return merged

From split to merge. Knowing how to split and how to merge, we have the pieces we need for a divide-and-conquer sort, but how do we identify when to transition from splitting to merging? Well, we know the conditions that need to be true to use merge: it can begin once we have nothing but sorted lists. This means that the question we really want to answer is, “Without checking the order of its elements, how small a list must split produce before we know without checking that a list is sorted?” If we answer this question, then we’ve identified when we can stop splitting and start merging.

Did you figure it out? The key here is to think about the length of a list. Empty lists and lists with a single element are guaranteed to be sorted. Nicely, our merge function properly handles lists of these lengths.

We now understand the full divide-and-conquer method of sorting, which computer scientists call merge sort. The algorithm is easy to describe:

1. Repeatedly split unsorted lists in half. It’s fine if one “half” is one element larger than the other.

2. When split has reached the point where all lists are of length 0 or 1, stop splitting and begin merging.

3. Repeatedly merge pairs of sorted lists until only one list remains.

Iterative merge sort. All that’s left for us to do is translate this pseudocode into Python, which we’ll do twice. The code block below implements the merge-sort algorithm using while-loops, which computer scientists call an iterative approach. It’s not pretty, and it fakes the splitting part. By this, I mean that we know we’re going to split the original list all the way down until we have lists of length 0 or 1, and so the code just goes there. Line 15 implements all that work in one simple assignment. The function then iteratively merges adjacent pairs of sublists. Inside the innermost while-loop, it calls our earlier function merge.

### chap12/imerge_sort.py

def merge_sort(s):
    """Iterative merge sort: s sorted in place"""
    
    # Catch trivial cases (i.e., lists that are guaranteed to be sorted)
    if len(s) < 2:
        return
    
    # Imagine a splitting process all the way down
    # to sublists of length 1, which will then
    # grow back up to len(s) in powers of 2
    sublist_len = 1
    
    # Merge all sorted sublists back up the tree of splits
    while sublist_len < len(s):
        # i is the starting index of the next two sublists to merge
        i = 0
        
        # Merge all pairs of sorted sublists of length sublist_len
        while i <= len(s):
            # Compute the end index of the first sublist
            j = i + sublist_len
            # Catch the special case of the last sublist's length
            # that may be shorter than sublist_len
            k = min(j + sublist_len, len(s))
            
            merged = merge(s[i:j], s[j:k])
            
            # Put the merged list back into s
            ii = i
            for item in merged:
                s[ii] = item
                ii += 1
            
            # Move to the next pair of sublists to merge
            i += sublist_len * 2
        
        # Increase the length of the sublists to merge
        sublist_len *= 2

You Try It

The function merge_sort in imerge_sort.py implements the merge-sort algorithm using the hammer of iteration. It works, but as we’ll soon see, it is not the best tool for the job. Nonetheless, the next code block exercises this implementation, and I encourage you run it as you read through the code. While these blocks don’t contain any new Python syntax, this iterative implementation does a lot of hard-to-follow slicing in a pair of nested while-loops. You might drop in a few print-statements to make it easier for you to understand its work.

### chap12/imerge_sort.py

# Test merge_sort using our unsorted lists
a, c, w = unsort()
merge_sort(a)
merge_sort(c)
merge_sort(w)
print(f'a = {a}\nc = {c}\nw = {w}')

Recursion. Despite the ugliness of the iterative implementation, merge sort is typically faster than insertion sort. Given a list of \(n\) elements, insertion sort has a worst-case computational complexity of \(O(n^2)\) and merge sort of \(O(n log_2 n)\). This is because merge sort makes \(O(log_2 n)\) splits and this same number of merges, and each merge step requires \(O(n)\) work. On sorting a large list, this complexity difference is significant.

But it’s beginning to appear that to run faster, we must pay for this speed boost with a more complex implementation. Just eyeball insertion_sort versus merge_sort and recall what we saw in comparing bf_strmatch against rk_strmatch. Despite these two examples, we’ll see it’s not always true that increased speed begets an ugly implementation. Sometimes we just need to use the right tool, and for divide-and-conquer algorithms, that tool is recursion.

Recursion is a fancy way of saying that a function repeatedly calls itself. While having a function call itself in this manner may sound like a recipe for an infinite loop, we avoid this outcome by:

1. Requiring each recursive call to solve a slightly smaller (or simpler) problem, and;

2. Making sure we have one or more of what are called base cases, which do not involve a recursive call.[8]

Before we look at the recursive form of merge sort, let’s get a feel for the structure of a recursive implementation by looking at the canonical recursive algorithm: factorial. You probably remember that the factorial of a number \(n\), expressed in mathematical notation as \(n!\), is the product of the numbers between \(n\) and \(1\), inclusive.

We can directly calculate the factorial of a number like 4 by computing:

factorial_of_4 = 4 * 3 * 2 * 1

But we can also express it as:

factorial_of_3 = 3 * 2 * 1
factorial_of_4 = 4 * factorial_of_3

Using this idea, let’s assume we have a function factorial that takes a single input parameter n and returns its factorial value. Then the following equality would be true for any positive integer:[9]

factorial(n) == n * factorial(n - 1)

This is a divide-and-conquer approach, albeit unbalanced in its split. Nonetheless, it nicely illustrates recursion. We are basically saying, “If I knew the factorial of n - 1, I could compute the factorial of n with one multiplication.” In general, we don’t and so we call the function factorial from within itself (recursion!) to determine what the answer to this slightly smaller problem is.

From this, we can begin writing the implementation of the factorial function.

def factorial(n):
    return n * factorial(n - 1)

This function matches our earlier description, but what happens when we call factorial(4)?

You Try It

While you can write yourself a short script containing the previous code block and a call of factorial(4), it is more informative to watch each step of the function’s execution using the Python Tutor: https://bit.ly/ctps-factorial4

What’s missing, of course, are the base cases. To add the base cases to our function, we need to know for what values of n do we know factorial(n) without having to compute it. Or equivalently, for what values of \(n\) is it trivial to compute \(n!\)?

Right! By definition of the mathematical function, we know that \(1!\) and \(0!\) are both \(1\). If we checked the input parameter n to see if was 0 or 1, we could skip the recursive call and just return the known answer. The following is a complete and correct recursive implementation of factorial. You can check this implementation with a few unit tests in the subsequent code block.

### chap12/factorial.py

def factorial(n):
    if n == 0 or n == 1:
        return 1
    elif n < 0:
        raise ValueError('factorial is defined only for positive n')
    return n * factorial(n - 1)

### chap12/factorial.py

# Test code
print('Testing factorial ...')
assert factorial(0) == 1, 'Failed for n = 0'
assert factorial(1) == 1, 'Failed for n = 1'
assert factorial(2) == 2, 'Failed for n = 2'
assert factorial(3) == 6, 'Failed for n = 3'
assert factorial(4) == 24, 'Failed for n = 4'
assert factorial(16) == 20922789888000, 'Failed for n = 16'
print('PASSED our unit tests!')

Congratulations! You just wrote your first recursive program.

Iterative factorial. I mentioned that factorial was the canonical example of a calculation that can be solved by divide-and-conquer and implemented in a recursive style, but you might wonder what this function looks like if written using an explicit looping statement.

You Try It

Try writing the function factorial using either a for- or while-loop. You can find my for-loop solution in ffactorial.py and my while-loop solution in wfactorial.py.[10]

Notice that both of these iterative solutions require us to create a named temporary, which I called result in both solutions. This temporary exists in the recursive version of the code as the returned result from each recursive call. You can see this by watching the execution of our complete recursive factorial function on Python Tutor.[11]

Recursive merge sort. You might prefer the simplicity of the code in factorial over the other two implementations. And if you are inclined to think mathematically, this implementation clearly reflects the problem’s mathematical formulation, which might make this code easier for you to read and understand.

This simplicity of expression is a characteristic of recursive code, and it is why there are quite a few people who speak with a religious fervor about recursion. But it is true that this simplicity-of-expression quality becomes more evident as the divide-and-conquer problems we’re trying to solve become more complex. Let’s keep this in mind as we look at the recursive solution to merge sort.[12]

### chap12/merge_sort.py

def merge_sort(s):
    """Recursive merge sort: returns a sorted list"""
    
    # Catch trivial cases (i.e., lists that are sorted by definition)
    if len(s) < 2:
        return s
    
    # Find index at truncated midpoint of list
    mid = len(s) // 2
    
    # Return merge of the two sorted halves
    return merge(merge_sort(s[0:mid]), merge_sort(s[mid:]))

Are you thinking, “That’s it? Where’s the rest of the code?” There is no more code. That’s all it takes to write merge sort recursively.

Not sure? Let’s test it.

### chap12/merge_sort.py

# Test merge_sort using our unsorted lists
a, c, w = unsort()
aa = merge_sort(a)
cc = merge_sort(c)
ww = merge_sort(w)
print(f'a = {aa}\nc = {cc}\nw = {ww}')

What do you think now about recursion as a way of expressing a problem’s implementation? As you can see, it works extremely well for problems that are amenable to divide-and-conquer solutions. Interestingly, a large number of problems in math and nature are neatly expressed in recursive formulations because we can solve them with induction, which is what we saw in our recursive solution to factorial.

Beckett’s challenge. As promised, this chapter ends by solving a problem that doesn’t seem like it is amenable to a divide-and-conquer approach. Now, I don’t expect you to see the solution before it’s presented. I don’t even expect you to feel comfortable with the solution after you’ve played with its recursive implementation. It takes time and repeated practice to think in this way, and you’re probably still striving to be comfortable building iterative solutions. I simply ask you to work through this final problem and appreciate the power of the approach and the simplicity of the solution. And then remember this technique when you’re solving your own problems.

Since this book has a theatrical theme, we’re going to investigate a problem posed by the playwright Samuel Beckett.[13] One of his plays, named Quad, has the actors enter and exit the stage so that the same subset of actors never appears together more than once.[14]

What does this mean? Let’s imagine a play with three actors, named A, B, and C. As the play begins, the curtain rises on an empty stage. We’ll represent an empty stage by placing a 0 under each of the actors’ names. Then, when actor enters the stage, we’ll change their 0 to a 1. When they exit, their 1 becomes a 0. Only one actor will enter or exit the stage at any instance in time.

Under these constraints and with these encodings, Figure 34 illustrates a solution to Beckett’s challenge for our three actors A, B, and C.

Fig. 34 A solution to Beckett’s challenge with three actors.

This table contains eight rows (not counting the header) because the number of different subsets of \(n\) objects is exactly \(2^n\). To verify that this table, when reading the rows in order from top to bottom, is a solution to Beckett’s challenge, notice that, when looking at the ABC binary encodings, no two rows of the table are the same, which means that no subset of actors is on the stage more than once.

Its base case. To create a script that can solve Beckett’s challenge for any number of actors, we must first choose a divide-and-conquer approach. You’ve seen two different divide-and-conquer examples, and let’s try the approach we took in factorial. Recall that it wrote an expression for the factorial of a number using the factorial of the number that was one less. Perhaps we can solve Beckett’s challenge with n actors by assuming we know the solution to the challenge with n-1 actors.

Hmmm. It’s not immediately obvious to me what stage directions we need to add to the solution with n-1 actors that produces the solution with n actors, and so let’s try some simple examples. What would we print for stage directions to solve Beckett’s challenge for a play with no actors? It is the smallest Beckett challenge, and it feels like our base case.

Do you see that we’d print nothing for a challenge involving zero actors? We have an empty stage, and no actors to enter or exit it. During the recursive call sequence, when we’re calling our function with ever smaller problems, this is our recursive function’s base case. Let’s start writing our function beckett so that it prints nothing and returns when called with no actors.

### chap12/beckett0.py

def beckett(n):
    """Given n actors, print stage directions"""
    if n == 0:
        return

The play with a single actor. Beckett’s challenge with a single actor should print the first two lines in Figure 34. The first line is a unique stage direction, and we want it printed even in the challenge with no actors. But we don’t want "empty stage" printed in the base case of the recursion; it should be printed only at the start of a challenge. This reasoning leads us to put this print-statement in the function that calls beckett and starts the recursion.

Inside our current beckett function, we have the base case, and we need to add a recursive call and the print-statement that outputs "enter 1" for our current example.[15] A base case, a recursive call, and some problem-specific work is what constitutes the normal structure of a recursive function. But where does the recursive call go? Before or after our print-statement? You can see for yourself that either case correctly prints what we want for challenges with 0 or 1 actors.

### chap12/beckett1.py

def beckett(n):
    """Given n actors, print stage directions"""
    if n == 0:
        return
    
    beckett(n - 1)     # recursive call here?
    print('enter', n)
    # beckett(n - 1)     # or here?

# Test with 1 actor
num_actors = 1

print(f'empty stage')

beckett(num_actors)

Looking for the pattern. To design an algorithm that generates stage directions of the form “enter B” and “exit C” for the play in Figure 34, we must identify and understand the repeating patterns in the table’s sequence of binary encodings. In general, coding with recursion involves finding the pattern that repeats, each time on a smaller scale. Let’s focus on the solution table for the challenge with two actors.

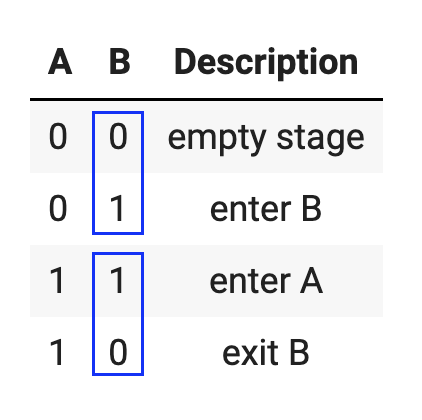
Fig. 35 A solution to Beckett’s challenge with two actors.

In Figure 35, what do you notice about the sequencing of the bits for actor B? Compare the first two boxed values against the last boxed two. Yes! The sequence reverses itself.

Now look at actor A. They act like an actor in the one-actor challenge: Halfway through the play they enter and never exit. But this halfway point is far enough into the play that actor B has time to go through a 0-1 dance. And once A enters, they wait patiently as actor B reverses their dance from the first half.

With that pattern in mind, look back at Figure 34. Actor A enters halfway through the play. When they enter, actors B and C had enough time to go through a dance, which these two actors reverse once A enters. And the dance that B and C do in the first four rows is the same dance they did in the 2-actor challenge. We’ve found a pattern to exploit![16]

A polished, full solution. With the pattern recognized, what remains is to convert the pattern into code. While I won’t take you through the details, I will highlight a few interesting aspects that we didn’t see in factorial or merge_sort.

• beckett needs to make two recursive calls corresponding to the dance A watches off stage and then the dance this actor watches while on stage. The same is true for every actor.

• The printing goes between the two recursive calls, which means that we had the right idea in beckett1.py, even if we didn’t realize it at the time. You can see this by focusing on actor A, who we just discussed watches off-stage as the other actors go through their dance (i.e., the first recursive call). Actor A then enters the stage (i.e., we print "enter A"). And finally, this actor watches on-stage as the other actors go through their reversed dance (i.e., the second recursive call).

• We need to send along another piece of information, which is a Boolean telling the recursion whether an actor is in the “dance-in” or “dance-out” portion of their pattern. This is the purpose of the enters parameter on beckett.

### chap12/beckett32.py

# Set the number of actors in your play, which
# must be less than or equal to 10
num_actors = 3
assert num_actors <= 10

# Setup for pretty printing
on_stage = 0  # encoding of who is on stage
if num_actors == 3:
    # Used to demonstrate the dance with playing cards
    names = 'KQJ'
else:
    names = 'ABCDEFGHIJ'[:num_actors]

def stage_print(dir, n):
    global on_stage
    if dir == 'enter':
        on_stage += 2 ** (n-1)
    else:
        on_stage -= 2 ** (n-1)
    print(f'{bin(on_stage)[2:].zfill(num_actors)} {dir} {names[num_actors - n]}')
    
def beckett(n, enters):
    if n == 0:
        # No characters so no stage directions
        return
    
    beckett(n - 1, True)
    if enters:
        stage_print('enter', n)
    else:
        stage_print('exit', n)
    beckett(n - 1, False)

# Start printing the solution table
print(f'{bin(on_stage)[2:].zfill(num_actors)} empty stage')
beckett(num_actors, True)

This final beckett function is disturbingly simple, and that’s what happens when the pattern embedded in the problem is matched with the right tool. In this case, the tool was a divide-and-conquer approach coupled with the technique of recursion.

I hope you understand how the recursive beckett function works. I hope you’ve also begun to realize that learning to write a recursive function from a recursive specification, like we did with factorial and merge sort, is hard but worthwhile. Designing a recursive solution to a problem like Beckett’s challenge is even harder, but you can do it if you take it a step at a time, as we just did.

---

[1]

Divide and conquer is sometimes called divide and combine, a name that highlights the two pieces of this problem-solving process.

[2]

I’ve borrowed this definition from Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest, Introduction to Algorithms (Cambridge, MA: MIT Press, 1995), 2.

[3]

To learn more about sorting in Python, please see the helpful page titled “Sorting Techniques” by Andrew Dalke and Raymond Hettinger. https://docs.python.org/3/howto/sorting.html

[4]

Letters are sorted from a-z, except that capital letters are “smaller in value” than little letters. Letters that represent positive numbers are sorted in numerical order. Unicode characters are sorted by their numerical values. In fact, sorting letters and numbers are also explained by the realization that we’re just sorting unicode values! Look up the unicode values of the characters A, B, a, b, 0, and 1.

[5]

The largest number of swaps occurs when the input sequence is the reverse of the sorted order, e.g., `[5, 4, 3, 2, 1]`.

[6]

A simple internet search for “sorting algorithms” will list many of the most popular sorting techniques.

[7]

As another example of binary search in action, watch Professor David Malan of CS50 fame use binary search to find this book’s author in an old-fashioned phone book. https://www.youtube.com/watch?v=DSffdCT5Cx4

[8]

It might help to have an image of the Russian Matryoshka Dolls (https://en.wikipedia.org/wiki/Matryoshka_doll) in your mind. Each inner doll is smaller than its outer doll, and if you open them all, you’ll find that the innermost doll doesn’t open. That innermost doll is the base case.

[9]

Factorial is defined only for non-negative integers.

[10]

As expected, when compared to the for-loop solution, the while-loop solution requires us to manage the loop’s index variable. My while-loop solution reuses the input parameter as the while-loop’s index variable to save one initialization. Nothing new here.

[11]

https://bit.ly/ctps-factorial4correct

[12]

The recursive solution will use the same `merge` function that we used in the iterative solution, but I will slightly change its interface. While the iterative solution sorted the input list in place, it is more natural for the recursive solution to return the sorted list. This has to do with the lack of an explicit temporary, which we noticed in looking at the several factorial implementations.

[13]

https://en.wikipedia.org/wiki/Samuel_Beckett

[14]

I learned about this challenge from Robert Sedgewick and Kevin Wayne, Computer Science: An Interdisciplinary Approach (Boston, MA: Addison-Wesley, 2017), 275. It appears as Program 2.3.3.

[15]

Let’s not worry about printing the actor’s names, which is a detail we’ll fix when we have a correctly working recursive function.

[16]

The binary sequence produced by the function `beckett` is called a Gray code (https://en.wikipedia.org/wiki/Gray_code), which has found many uses in our world, from electronic devices to experimental design. Now that you know about this code, read about it and look for it in your world!