Chapter 9: Find a Phrase

The first act introduced fundamental ideas in problem solving with computers, and it set the stage for the conflict revealed in this second act: The world is a wondrously complex place. If you do not manage this complexity in a systematic way, it will overwhelm you.

Luckily, through your work in Act I, you have already begun using the most-important tools of computer science—decomposition, abstraction, and encapsulation—to systematically manage a complex world with complex problems. This act dives deeper into the power of these tools, and it illustrates how you can elegantly manage nearly any amount of complexity the world throws at you.

A complex problem-to-be-solved. We’ll start with a theme you may have noticed in the previous act’s problems. We asked if we could find a double-quote character in a string and the words “cat” and “hat” in a text file. We asked if we could find a particular book in the Harvard Library. And in the previous chapter, we talked about the importance of looking for particular patterns in a sea of numbers. These are all examples of search problems.

Search appears in almost all aspects of our personal and professional lives, making it a nearly ubiquitous technique in problem solving. Looking across time at the characteristics of our search problems, we see a fascinating trend: the data over which we search has consistently grown in size. Fueling this has been a relentless growth in the capabilities of our computers, which allow us to solve ever larger search problems in ever shorter amounts of time. This human desire to find answers to our questions ever more quickly has become, in fact, a big business.

In Google’s “home” movie about its beginnings and its mission, it mentions that it took King Louis XIV in 1685 about the 5 years, 4 months, and 2 days to get an answer to his question about the Qing Dynasty.[1] Today, Google and other search engines like it report such answers in under a second, as illustrated in Figure 21.

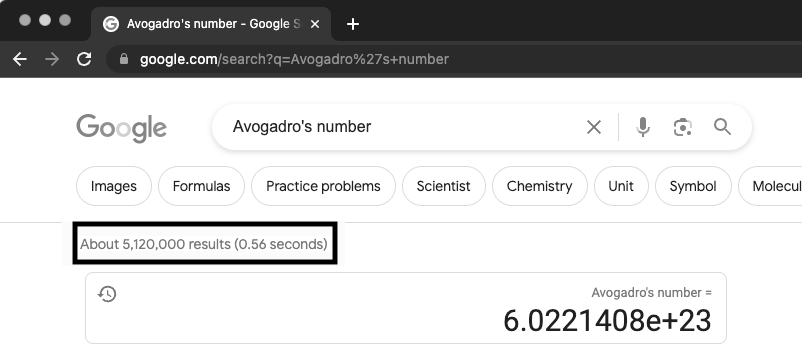
Fig. 21 Highlighted in the black rectangle is the amount of time it took me in 2023 to run a search for Avogadro’s number on Google.

What specifically is the Google search problem? Well, Google’s mission is “to organize the world’s information and make it universally accessible and useful.”[2] They’re specifically talking about information that individuals and corporations around the world publish in electronic form on the Internet. Ideally, Google wants to understand the questions we have and serve us the most relevant information it has found.

This is quite a hard problem. It involves natural language processing (NLP)[3] and the use of other contextual information to understand exactly what we want (or might likely want) to know. In searching for answers, we expect Google to understand all types of digital information, including webpages, images, videos, podcasts, and other types of standardized file formats. We expect Google to highlight the most relevant answers and sift out the dreck. And, of course, Google as a for-profit company should find some way to earn money while doing this.

We’ll get to many of these issues in this act, but to begin, let’s simplify and focus where Google started: how do we make it easy to find the webpages that mention a particular word or phrase? We won’t build our own web search function, but we will determine what it would take to write a script that finds and returns a listing of all pages on the World Wide Web containing our search phrase.

Learning Outcomes

In this chapter, you will learn about the ubiquity of search problems and dive into the details of Google search. You will understand the difference between algorithms and formal specifications. You’ll investigate several ways to do string matching and measure the performance of each. You’ll learn to evaluate an algorithm without having to run it by roughly calculating its computational complexity. By the chapter’s end, you will be able to:

• Learn to estimate the size of your problem [design];

• Understand the different, formal aspects of an algorithm [design and CS concepts];

• Write a formal specification for string matching [design and CS concepts];

• Discuss the differences between algorithms and specifications [design];

• Recognize brute-force algorithms and whether they’re a sufficient solution or not [design];

• Identify when different programs all implement the same algorithmic approach [design and CS concepts];

• Evaluate and measure the performance of a program [CS concepts and programming skills];

• Use the tool of computational complexity to compare two algorithms [CS concepts].

Some basic facts. What do we know about the Google search problem? First, we can learn that webpages are simply text files written with a particular structure and adhering to one of several Web standards. Since we are not worried about how they are rendered by a web browser but only what words they contain, we can mostly ignore the specifics of these standards and treat webpages as simple text files, like the ones we saw in Chapter 1.

We can also discover that there are a lot of webpages out there. Google says that its search index “contains hundreds of billions of web pages and is well over 100,000,000 gigabytes in size.”[4] Let’s not worry about what Google means by its “search index,” and let’s just keep in mind that there are so many webpages out there that they might be a challenge for our script to process.

Finally, from our own experience surfing around the web, we know that individual webpages come in a wide range of sizes, where we measure size in number of characters. Many pages, however, are not much longer than a short story. In other words, it is probably the size of the total search, and not the search on any one webpage that will challenge us.

Altogether, this information tells us a lot about the input to our problem.

Which algorithm? Now that we’ve thought about the input data, what can we say about the algorithm that will consume these data? We used several ways of finding a target string in some larger input string in Chapter 2.[5] We could iteratively read each webpage as a string and use one of these to determine on which pages our search phrase occurs. We’d then collect and return a list of all these webpages.

While this would work, we might want to know more. For example, we might also wish to know where on the webpage the search phrase was found, which means we want to use something like Python’s string-find method. And beyond a question of functionality, we don’t know anything about how Python has implemented any of its approaches.

Unlike the first act, we now want to do more than just find a solution to our problem. We want to learn how to evaluate several different algorithms so that we can determine which does what we need and works reasonably well under the problem’s conditions. Only then will we be sure that we’ve truly solved our problem for the use cases that concern us.

Algorithms, formally. Boaz Barak, a brilliant colleague of mine at Harvard, says that algorithms have three formal components: (1) a specification; (2) an implementation; and (3) a proof of correctness.

In Act I, we focused largely on an algorithm’s implementation, which is a step-by-step description of how the algorithm accomplishes its task. But what task is that? This is the job of an algorithm’s specification. When given a precise specification of the behavior we would like to see in an algorithm’s implementation, there are techniques we can use to verify that the how satisfies the what. In fact, there exists a whole field of formal verification concerned with the matching of software implementations against their specifications. When this matching succeeds, computer scientists say that the implementation has been proven to be correct.

We won’t concern ourselves with formal proofs of correctness, but we do need to stop being so loose in our specification of what our algorithms should do. By separating specification from implementation, we can compare two different solutions, which might match in their what but not their how. Sometimes we are happy to pay for more what (e.g., knowledge of not just that a search phrase exists on a webpage, but how many times and where it appears on each page). Other times, we want one particular what, and for two algorithms with a shared specification, we might be interested in the differences in the how of each (e.g., without any differences in what they do, which runs fastest given a particular input).

A well-studied specification for string matching. Let’s decide upon a specification for our current problem-to-be-solved. This won’t be hard because lots of programs we use every day frequently need to find the locations of one string within another. It’s not just web search engines. Think about how many times you run a program and “find” is a command under the “edit” menu. Because this functionality is so important to so many applications, string matching has been a well-studied problem in computer science.

In their popular text titled Introduction to Algorithms, the authors state a formal specification for string matching, which we’ll use.[6] It first describes the two inputs to the problem: a text array T[1..n] of length n and a pattern array P[1..m] of length m ≤ n. It then defines a property called a valid shift s, which is an integer between 0 ≤ s ≤ n – m where T[s + 1..s + m] = P[1..m]. An algorithm satisfies the string-matching problem given text T and pattern P if it can find all valid shifts of P in T.

In terms of our web search problem and Python data types, P is a Python string we typed in the Google search box, whose location we want to find in every webpage known to Google. T is also a Python string, and we can think of it as the concatenation of the text of every webpage known to Google. Each valid shift s is an index into T where we can find the start of an instance of P.

Be careful with the index notation here. The specification numbers the characters in T and P starting at index 1, which is common in formal languages that describe the behavior of something. The first character of P is P[1], and this character can be found at T[s + 1] for any valid shift s. This is why the string-match equality might look a bit strange to your mind that has gotten used to 0-based indexing. When we implement this specification in Python, we’ll switch from 1-based to 0-based indexing.

Is a specification an algorithm? Be careful not to fall into the trap of thinking that a specification is an algorithm. Someone might give you a specification that contains statements of how among the what, but specifications need only describe behavior.

In textbooks that teach you to program, you’ll often see a picture like the one in Figure 22, where the black box is labeled with the text “algorithm” or “program.” This sort of picture is simply a graphical depiction of a specification. Specifications tell you what output you’ll get for each input. Good specifications tell you how the black box behaves on all inputs and when it’s given no input.

Fig. 22 The canonical illustration of an algorithm (or program).

The box is often colored black because you’re supposed to think of the box as opaque. It is easy to imagine an opaque box hiding the algorithm that implements the specification (or the program that implements the algorithm that implements the specification).

However, as we will see in Chapter 14, we can have a specification that can’t be implemented by any algorithm. (Just trust me at this point. We’ll prove it later.) This means that we can draw every algorithm and every program with this type of picture, but we cannot take every picture describing a specification and find an algorithm or write a program for it. Yes, the world is strangely beautiful.

A brute-force algorithm. Let’s now create an algorithm for this string-matching specification. We will take advantage of the fact that today’s computers are amazingly powerful and never get bored, which means that we can assign them a crazy amount of work and they’ll do it without complaint. This is called a brute-force approach to problem solving, and it sometimes works just fine. It has the computer explore the entire space of possible solutions, flagging those that solve our problem.

The following pseudocode[7] describes an algorithm for brute-force string matching (BF_STRMATCH):

# BF_STRMATCH(t, p)
# inputs are the text t and the pattern to match p
# n = length of t
# m = length of p
# for s = 0 to n - m:
#     if p[0:m] == t[s:s+m]:
#         print "Pattern occurs with shift" s

This particular algorithm closely follows the one given in Section 32.1 of Cormen et al. [2009], where the authors describe this brute-force algorithm as implementing the pattern as a template slid along below the text (see Figure 23). When the characters in the text above the template match those at each location in the template, the algorithm announces the number of uncovered characters from the start of the text as a valid shift.

Fig. 23 An illustration of the BF_STRMATCH algorithm, in which it slides the pattern string along the text string looking for exact matches. When it finds one, it announces the shift from the start of the text string where the match occurred.

This is a very simple solution to our string-matching problem, and something each of us has probably done at some point when trying to find the last few words in a word-find puzzle. We do it last because it’s tedious to check each starting location and whether the letters at that starting location exactly match each letter in the pattern word. Of course, if we persevere and get to the end of the puzzle, we are rewarded by knowing that we’ve considered every possible location, and that there cannot be anymore instances of the pattern in the input text. For these human and technical reasons, people also call brute-force approaches exhaustive approaches.

A BF-string-matching program. Since we’re not going to formally prove that our BF_STRMATCH algorithm implements our string-matching specification, let’s implement this algorithm in Python and run a few test inputs. This doesn’t guarantee that our algorithm is correct in all cases, but it gives us some assurance that we’re not missing something obvious.

The translation from pseudocode to Python is straightforward, especially given the simplicity with which we can specify string comparisons in Python.

### chap09/bf_strmatch.py
def bf_strmatch(t, p):
    n = len(t)
    m = len(p)
    for s in range(n - m + 1):
        if p[0:m] == t[s:s+m]:
            print(f'Pattern occurs with shift {s}')

Now let’s run a few tests.[8]

t = 'This is a test.'
p = 'test'
bf_strmatch(t, p)

Counting the number of characters before the start of the occurrence of p in t shows that our code works on this simple example.

Will our function work with a longer test string and multiple matches?

t = 'This test is a longer test.'
bf_strmatch(t, p)

So far so good. As we discussed in Act I, it’s always good to check what are called edge cases: Can we find a pattern string at the start or end of the text? What happens when the pattern doesn’t occur in the text? Does a space work as a pattern string? What does an empty pattern string match? Does our script find overlapping matches? You might try your own tests to see if you can break this implementation.

t = 'This test is a longer test'
p = 'est'
bf_strmatch(t, p)

p = 'This'
bf_strmatch(t, p)

p = 'this'
bf_strmatch(t, p)

p = ' '
bf_strmatch(t, p)

p = ''
bf_strmatch(t, p)

t = 'This teeest is a longer test'
p = 'ee'
bf_strmatch(t, p)

One algorithm, multiple implementations. Our Python implementation bf_strmatch is not the only Python code capable of implementing the algorithm BF_STRMATCH. The following function also implements our algorithm:

### chap09/bf_strmatch2.py
def bf_strmatch2(t, p):
    n = len(t)
    m = len(p)
    for s in range(n - m + 1):
        for i in range(m):
            if p[i] != t[s+i]:
                break
        else:
            print(f'Pattern occurs with shift {s}')

You Try It

Take a moment and compare bf_strmatch against bf_strmatch2. I’ve changed the body of the for-s loop. This body is simply a different way of comparing the pattern against the characters at each starting point s in t.

Let’s run our last test again to make sure this new version operates correctly. Feel free to try any of the other tests too.

t = 'This teeest is a longer test'
p = 'ee'
bf_strmatch2(t, p)

The point is that a single algorithm can have many programming language implementations. We created two in Python, but we also could have used any other programming language to create an alternative implementation.[9]

Evaluation. Which Python implementation, bf_strmatch or bf_strmatch2, do we prefer? Well, what are our criteria for preferring one implementation over another?

One obvious criterion jumps out when we look at these two Python functions: bf_strmatch requires fewer characters than bf_strmatch2. That might be a good reason to choose the first over the second.

Of course, it is possible to go too far in this direction. The more shorthand notations we use the more knowledgeable our reader must be. You’ve probably encountered this at a lecture where the speaker assumes the entire audience is comfortable with the discipline’s lingo. If you’re not, you quickly lose any idea of what the speaker is talking about.

We may not care about a single criterion, but multiple criteria and the tradeoffs between them. For example, we strive to write bug-free scripts, and some programming languages constrain the types of values a variable can hold so that you can use specialized tools to identify hard-to-find bugs.[10] This approach trades one criterion (i.e., shortness of our scripts) for another (i.e., ease of finding bugs).

In general, there are many criteria on which we might judge one implementation against another. Correctness is clearly a necessary criterion, but not the only one you may care about. Which other criteria matter depends on your problem-to-be-solved.

Evaluation in context. We have a context for our string-matching script, and we can ask, “Will brute-force string-matching work for Google Search?” Well, which evaluation criteria matter most (besides correctness) in this context?

At the start of this chapter, we mentioned that people expect answers to their search questions in ever shorter amounts of time. Therefore, in this context, we care about how quickly a script’s implementation can return an answer.

Overall, the performance of an algorithm and its implementation is one of a handful of questions that computer scientists ask all the time. Does the algorithm solve our problem of interest? If yes, does it run correctly under all input conditions? If yes, how fast does it run? How much space (e.g., computer memory) does it use while running? Is it resilient to adversarial attacks? We will cover most of these questions and say a few words in the next act about the historical importance of the last few. But for now, we will focus on answering the question of how long an algorithm (or the script that implements it) takes to run, since that’s important in searching 100 million gigabytes of text.

Measuring performance. Asking how long a script takes to run seems like a straightforward question: Go grab your smartphone, launch the stopwatch app, start the stopwatch as you begin running the script, and stop it when the script completes. However, coordinating the starting and stopping of your stopwatch with the starting and stopping of a program is a bit tricky, and most operating systems provide you with a time utility that does this work for you.

To use this utility in the shell, you often type the name of the time utility and then the command you want timed. The next code block illustrates this and the result of using my operating system’s time utility[11] to measure how long it takes to run bf_strmatch and bf_strmatch2 with the same input.

chap09$ /usr/bin/time python3 bf_strmatch.py 'This test is a bigger test' 'test'
Pattern occurs with shift 5
Pattern occurs with shift 22
        0.05 real         0.02 user         0.01 sys
chap09$ /usr/bin/time python3 bf_strmatch2.py 'This test is a bigger test' 'test'
Pattern occurs with shift 5
Pattern occurs with shift 22
        0.05 real         0.03 user         0.01 sys

From the output, we see that our two scripts ran and produced the expected output. In addition, the time utility printed three different measures of the execution of each script, each measured in seconds. You can think of the first number, which is labeled real, as wall-clock time. It is the one that concerns us. We’re going to ignore the other two, which break wall-clock time down into two components that are not important to our current evaluation question.

Both scripts took 5 hundredths of a second to execute. If you run these two commands yourself, you’ll see the first number vary a bit. For instance, I got 0.08 seconds on one run, but most of my runs were 0.05 seconds. There was no discernible pattern that said one script was faster than the other.

Part of the problem here is that my computer is fast and the program doesn’t make it work too hard. How can we make my computer work harder to see if one script is actually faster?

That’s right. The script will run longer if we give it more text to search (e.g., War and Peace by Leo Tolstoy[12] or Just David by Eleanor H. Porter[13], both of which you can download from Project Gutenberg).

To this point, we’ve typed the text we fed to bf_strmatch.py and bf_strmatch2.py. Since we probably don’t have the time to type a long text, we’ll use the option of reading the text input from standard input (stdin) in a new way.[14] Using this method, our existing scripts can read the contents of the Project Gutenberg text files we download.

How does this work? In Python, sys.stdin is a file object like those we created with the open command, and on which, we can perform operations like read and readline. In bf_strmatch.py, when the script determines that we provided only the pattern on the command line, it calls sys.stdin.read() and assigns the returned string to t (see line 22).[15] Previously, this line read the text we typed, but on Linux-like systems, you can extend a command like python3 bf_strmatch.py 'test' with a less-than sign (<). After this less-than sign, you indicate the filename whose contents you want available on sys.stdin. As an example, the following code block runs bf_strmatch.py looking for the phrase 'has left' in the file JustDavid.txt.

chap09$ /usr/bin/time python3 bf_strmatch.py 'has left' < JustDavid.txt
Pattern occurs with shift 326953
        0.15 real         0.10 user         0.01 sys

This is still not a very big text, and the script runs in about 15 hundredths of a second on my computer.[16] However, the text is large enough to see that Python’s string comparison using the equal-equal operator (==) is slightly faster than our own for-loop comparison. We will talk about why this is true in Chapter 16, but for our purposes here, it’s enough to know that we’ve added work for the Python interpreter to do using our own for-loop in bf_strmatch2.py that doesn’t exist when we forego that for-loop and instead use the equal-equal operator built into the language.

Tip

If you want to feed the functions bf_strmatch and bf_strmatch2 some of your own big input text files and time them, the script chap09/cmp_bf_times.py on the book’s Github repository automates the comparison of the two scripts, given a pattern and a filename whose contents you wanted searched. It uses a method from the Python time module.

The key point here is that the wall-clock difference between bf_strmatch.py and bf_strmatch2.py isn’t the result of something inherent in our algorithm. It exists because of the choices we made when implementing the BF_STRMATCH algorithm. As we have briefly seen, we can eliminate this time difference with careful choices as we code our algorithms, if we understand what language features take what amount of time at execution. Again, a topic for later.

But let’s return to the real question: Should we use the BF_STRMATCH algorithm to search 100 million gigabytes of text every time a user types a search into Google? Let’s do some back-of-the-envelope calculations. If a 327-kilobyte text file (i.e., JustDavid.txt) took about 0.1 seconds to search, it will take my machine about 30 billion seconds to complete the Google search problem, because that input is approximately 300 billion times bigger (i.e., 0.1 seconds times 100 million gigabytes divided by 327 kilobytes). Google’s users don’t want to wait 30 billion seconds, or about 1000 years, for their answers. Even King Louis XIV wasn’t going to be that patient.

Certainly Google has access to machines faster than my laptop, but not 46 billion times faster. We need to find a different solution.[17]

How do we do better? If we want a script that solves our problem significantly faster, we need to realize is that our biggest gains will come from changes not to the coding of an algorithm’s implementation but to the algorithm itself.

Tip

If your script runs too slow, think about using a different algorithm. Coming up with new, efficient algorithms, however, is hard and most of us never try. What happens instead is that we attempt to reduce the most complex pieces of our programs to previously solved problems. This means that you should start your work by attempting to solve your problem in the most straightforward manner possible. Then measure the performance of the different parts of your script, and for the pieces that need to run faster, search for known algorithms that you can use to speed them up.

I said earlier that string matching is a well-studied problem in computer science, and some very smart people have come up with algorithms that are significantly faster than our brute-force technique. The following is a Python implementation of one called the Rabin-Karp algorithm.[18] You don’t have to understand the algorithm at this point; we’ll discuss its operation in the next chapter. Right now, I just want you to notice that its implementation takes more statements than our brute-force method. This raises the interesting question: What additional work have Rabin and Karp identified that creates an algorithm that runs faster than the brute-force approach?

### chap09/rk_strmatch.py
def rk_strmatch(t, p):
    n = len(t)
    m = len(p)
    
    # Preprocessing steps
    
    # Constants in Rabin-Karp string-matching problem
    d = 256    # number of character encodings in ASCII
    q = 65537  # a prime number
    
    # Compute the hash value of a 1 in the high-order position (i.e.,
    # m-1th position), where digits have radix d
    hh = 1
    for i in range(m - 1):
        hh = (hh * d) % q
    
    # Calculate the hash values for p and t[0:m], since the matching
    # loop needs these values as it starts
    hp = 0
    ht = 0
    for i in range(m):
        hp = ((hp * d) + ord(p[i])) % q
        ht = ((ht * d) + ord(t[i])) % q
    
    #print(f'DEBUG: pattern hash("{p[0:m]}") = {hp}')
    #print(f'DEBUG: hash("{t[0:m]}") = {ht}')
    
    # Matching step
    for s in range(n - m + 1):
        if hp == ht:
            # Verify that this is an actual match
            if p[0:m] == t[s:s+m]:
                print(f'Pattern occurs with shift {s}')
            #else:
                #print(f'DEBUG: hash collision')
                #print(f'DEBUG: hash("{t[s:s+m]}") = {ht}')
        
        if s < n - m:
            # Need to compute hash for next iteration
            ht = ((ht - (ord(t[s]) * hh)) * d
                  + ord(t[s+m])) % q
            if ht < 0:
                ht += q
            #print(f'DEBUG: hash("{t[s+1:s+1+m]}") = {ht}')

The following code blocks allow you to try the Rabin-Karp algorithm with some of our recent test inputs. Nothing too exciting here, as we’d expect it to produce the same output as our brute-force algorithm. Both satisfy the same specification.

t = 'This is a test.'
p = 'test'
rk_strmatch(t, p)

t = 'This test is a longer test.'
rk_strmatch(t, p)

p = 'This'
rk_strmatch(t, p)

t = 'This teeest is a longer test'
p = 'ee'
rk_strmatch(t, p)

Loops are where the action is. When we are concerned about performance, straight-line code may take some time to execute, but a script will typically spend most of its time executing in loops, especially when each loop index covers a large range. As such, let’s compare the looping structure in bf_strmatch with that in rk_strmatch. In particular, let’s abstract away most of the detail except for the loops and any conditionals protecting the execution of a loop. In some sense, we’re returning to pseudocode, but focusing our pseudocode not on function, but behavior.

def bf_strmatch(t, p):
    # some setup work
    # no loops
    
    # Matching work
    # loop on s up to n times
    #     loop up to m times checking for match
    #     if found-match print

def rk_strmatch(t, p):
    # some setup work
    # loop on i exactly m-1 times
    # loop on i exactly m times
    
    # Matching work
    # loop on s up to n times
    #     if two numbers match
    #         loop up to m times checking for match
    #         if found-match print
    #
    #     if not at end of s loop
    #         do some math; no loops

Importantly, both algorithms have a loop with index variable s that does some work for each possible shift value. Both these algorithms loop up to n (i.e., the length of the input text) times. They may loop fewer times, but in the worst case, they will loop n times when the length of the pattern string is 1.[19]

Before we focus on the internals of these two matching loops, which will help us to understand the difference between the two algorithms, let’s discuss how I came to the pseudocode statements corresponding to each algorithm’s setup work. Looking first at bf_strmatch, the code (lines 9-10) does a couple of simple assignments; there are no loops. The setup code in rk_strmatch (lines 15-36), in contrast, includes two loops on index variable i that loop almost exactly m (i.e., the length of the pattern string) times. Inside these, the algorithm does some simple math and makes an assignment or two. This analysis produces the pseudocode on line 3 of bf_strmatch and lines 3-4 of rk_strmatch.

With this difference in the setup behavior, bf_strmatch looks like it is going to be faster. In the worst case, it does some straight-line code and then loops roughly n times, while rk_strmatch loops to m twice and then loops to n.

Let’s turn this English into an arithmetic expression. Let’s say that a reasonable amount of straight-line work is proportional to one unit of execution time. A loop body without any loops in it (i.e., just straight-line code) would therefore also have a cost proportional to one unit of execution time. The cost of a loop and its body would simply be the execution-time cost of its body times the number of iterations we estimate that it will make.

With these simple rules, the estimated execution time of bf_strmatch would be proportional to 1 + n * something, where something represents the cost of the matching loop body, which we haven’t estimated yet. The estimated execution time of rk_strmatch would be proportional to 1 + (m-1) * 1 + m * 1 + n * a_different_something. Simplifying the expressions and dropping the “1 +” and “- 1” terms, which are swamped in the worst case by large m and n values, we get the estimated, worst-case execution time of bf_strmatch to be proportional to n * something and of rk_strmatch to be proportional to 2 * m + n * a_different_something.

Now, what are the estimated costs of the body of each algorithm’s matching loop? The body of the matching loop in bf_strmatch contains a loop with a simple body, and as such, something is m * 1, or just m, in the worst case. Remember that the ==-operator is doing work equivalent to the for-i loop in bf_strmatch2!

The body of the matching loop in rk_strmatch also contains a loop with a simple body that iterates up to m times, but this inner loop is protected by an if-statement (line 43).[20] Unfortunately, we don’t have enough information right now about the operation of rk_strmatch to estimate when the condition in this if-statement will be true. It might be true during just one of the total n iterations of the outer matching loop. Or it might be true on every iteration of the outer matching loop. In the first case, the execution time of rk_strmatch will be proportional to 2 * m + ((n-1) * 1 + 1 * m), or m + n when we ignore constants. In the second case, rk_strmatch looks a lot like bf_strmatch, but with more setup work. The dominant factor affecting the execution time in this case is n * m, or more precisely when n and m are both large: (n - m + 1) * m.

Computational complexity. This way of thinking gets away from the specifics of our machine’s hardware, the choices different designers make in creating a programming language, the performance of the interpreter and runtime system that help run our scripts, and lots of other small details that affect wall-clock runtimes but aren’t inherent in the performance of one algorithm versus another. Instead, this way of thinking focuses on a few characteristics of the input and how they influence the gross behavior of the algorithm.

This is all a long way of saying some things matter much more than others, and all we really care about here is that large inputs will take more time to process than small ones. We saw this in the rough analysis of our two string-match algorithms. In particular, we found that the runtimes of the two algorithms were proportional to the sizes of their inputs, i.e., m and n. And the magnitude of these numbers directly changed the running time of each algorithm through its looping structure.

If you continue in computer science, you’ll soon learn that this type of work is the domain of theorists interested in questions of computational complexity. These individuals ask how efficiently, in terms of time and space, an algorithm can compute a solution. They’re interested in finding a collection of expressions (or technically functions), as we did just a moment ago, that do a good job of describing the behavior of an algorithm as its input grows in size and complexity. For example, these functions might bound an algorithm’s running time from above (i.e., in the worst case, the algorithm’s running time won’t grow faster than a particular function) and from below (i.e., in the best case, the algorithm’s running time won’t grow slower than another, possibly the same, function).

The rules I described above are a simplified way of finding such asymptotic running times. Theorists often present the results of this type of analysis using what’s called big-O notation, which has you focus on the dominant terms in the expression describing, for instance, an algorithm’s running time.

The matching time of the algorithm behind bf_strmatch is \(O((n - m + 1) * m)\), which you should recognize as the expression we derived. It is also the worst-case matching time for rk_strmatch. This big-O notation means that, within some constant factor, there exists some numbers for \(n\) and \(m\) beyond which the growth of algorithm’s running time will not exceed the growth rate of this big-O function.

If you don’t understand all these details, that’s fine. I simply want you to identify these dominant terms in our algorithms and compare the growth rates for two different algorithms to see which is appropriate for your problem-to-be-solved.

Computational complexity in action. While we still don’t know how rk_strmatch finds matches in a cheaper manner than bf_strmatch, we have learned enough to manipulate the inputs to our two string-matching algorithms and see if we can experience the computational complexity differences we just computed. In particular, we expect to see the following:

• When \(m\) is small compared to \(n\), \(m\) will look like a constant factor in \(O((n - m + 1) * m)\), and the matching time of both algorithms will grow like \(O(n)\). In fact, bf_strmatch might outperform rk_strmatch since its extra setup work and extra work inside the matching loop may become noticeable.

• When \(m\) is a significant proportion of \(n\) (e.g., 25 percent of its size), \(O((n - m + 1) * m)\) will start to look more like \(O(n^2)\) for bf_strmatch. For rk_strmatch, how often the first if-statement within its matching loop evaluates true will dictate whether this algorithm grows as \(O(n)\) or \(O(n^2)\). We will assume that this if-statement evaluates true only when there’s an actual valid shift, and under this assumption, we will craft the pattern string so that it never matches, hopefully driving rk_strmatch toward \(O(n)\) growth as bf_strmatch experiences \(O(n^2)\) growth.

The following script implements this experiment using the content from JustDavid.txt. It concatenates copies of this file to create ever larger texts in which we look for either short or long patterns. In all experimental runs, the pattern never matches any of the text.

### chap09/cmp_strmatch.py
'''
Compares the brute-force and Rabin-Karp string-matching
algorithms across a range of input text and pattern sizes.
'''
import sys
import time
from bf_strmatch import bf_strmatch
from rk_strmatch import rk_strmatch

def compare_times(t, p):
    print(f'For p = {len(p)} bytes, t = {len(t)} bytes')

    start = time.process_time()
    bf_strmatch(t, p)
    print(f'bf_strmatch took {time.process_time() - start} secs')

    start = time.process_time()
    rk_strmatch(t, p)
    print(f'rk_strmatch took {time.process_time() - start} secs')

    print('')

def run_experiment(p_orig, t_orig):
    '''Call this routine with a reasonable search pattern that
       won't ever match in the text.'''
    # As setup, create p_big through repetition to be about
    # a quarter the size of the text input.
    p_big = p_orig
    while len(p_big) < len(t_orig) // 4:
        p_big += p_big

    # Number of tests to run, where each test is twice
    # as big as the last.
    times_to_double = 7

    print('### Test: len(p) << len(t)')
    t = t_orig
    p = p_orig
    for i in range(times_to_double):
        compare_times(t, p)
        t += t
        p += p

    print('### Test: len(p) < len(t)')
    t = t_orig
    p = p_big
    for i in range(times_to_double):
        compare_times(t, p)
        t += t
        p += p

def main():
    # Check for proper usage and grab the input strings
    if len(sys.argv) != 1:
        sys.exit("Usage: python3 cmp_strmatch.py")

    # Currently hardwired to grab the text from JustDavid.txt
    with open('JustDavid.txt') as f:
        t_orig = f.read()

    # A reasonable search pattern that won't ever match
    p_orig = 'David laughed softty'

    run_experiment(p_orig, t_orig)

if __name__ == '__main__':
    main()

This code, when run on my laptop, produced the following results, which I split into two columns corresponding to the two different tests.[21] Notice that I killed the script before it completed its run of the len(p) < len(t). I guess I have less patience than King Louis XIV.

### Test: len(p) << len(t)            ### Test: len(p) < len(t)
For p = 20 bytes, t = 327K bytes      For p = 82K bytes, t = 327K bytes
bf_strmatch took 0.065 secs           bf_strmatch took   0.785 secs
rk_strmatch took 0.156 secs           rk_strmatch took   0.136 secs

For p = 40 bytes, t = 654K bytes      For p = 164K bytes, t = 654K bytes
bf_strmatch took 0.142 secs           bf_strmatch took   3.199 secs
rk_strmatch took 0.289 secs           rk_strmatch took   0.289 secs

For p = 80 bytes, t = 1308K bytes     For p = 328K bytes, t = 1308K bytes
bf_strmatch took 0.255 secs           bf_strmatch took  13.314 secs
rk_strmatch took 0.570 secs           rk_strmatch took   0.551 secs

For p = 160 bytes, t = 2616K bytes    For p = 655K bytes, t = 2616K bytes
bf_strmatch took 0.503 secs           bf_strmatch took  53.569 secs
rk_strmatch took 1.125 secs           rk_strmatch took   1.114 secs

For p = 320 bytes, t = 5231K bytes    For p = 1310K bytes, t = 5231K bytes
bf_strmatch took 1.064 secs           bf_strmatch took 219.776 secs
rk_strmatch took 2.511 secs           rk_strmatch took   2.353 secs

For p = 640 bytes, t = 10462K bytes   For p = 2621K bytes, t = 10462K bytes
bf_strmatch took 3.707 secs           bf_strmatch took 890.305 secs
rk_strmatch took 4.611 secs           rk_strmatch took   4.560 secs

For p = 1280 bytes, t = 20926K bytes  For p = 5243K bytes, t = 20926K bytes
bf_strmatch took 5.858 secs           bf_strmatch took too long!
rk_strmatch took 9.736 secs

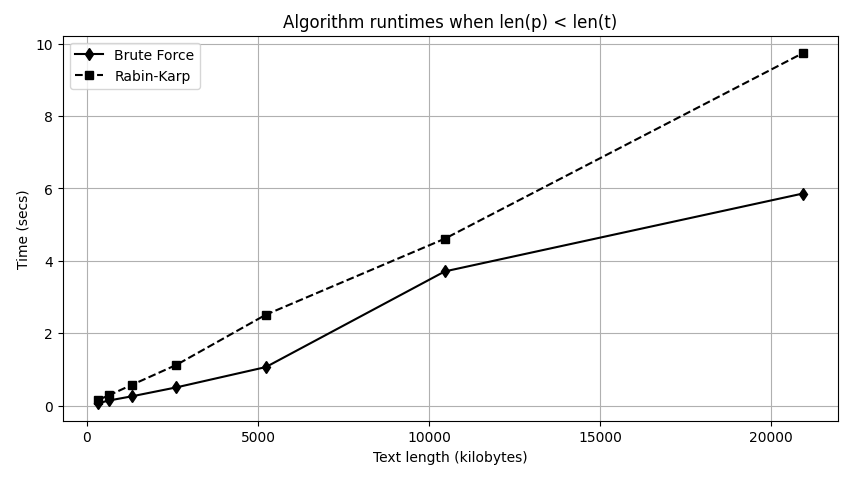
Fig. 24 Plot of the runtime of each script against the input text size (variable t) when the length of the pattern string is significantly smaller than that of the text string. The runtime of both algorithms grows linearly with the size of the input text.

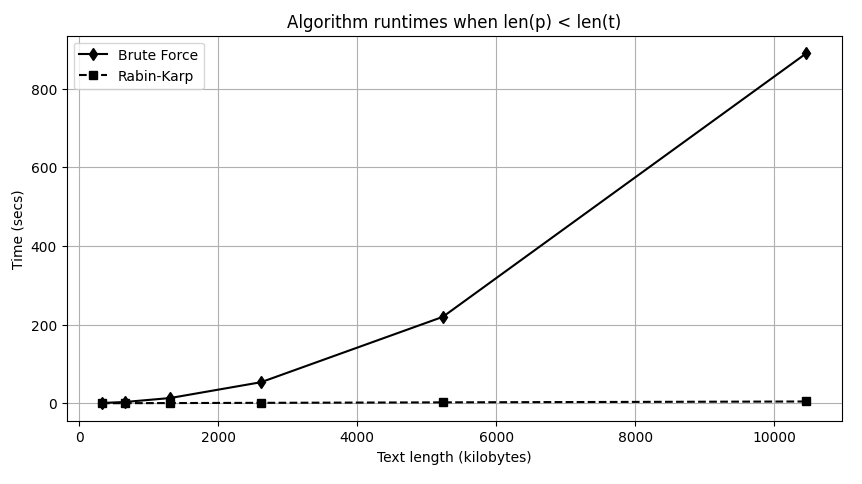
Fig. 25 Plot of the runtime of each script against the input text size (variable t) when the length of the pattern string is only slightly smaller than that of the text string. This time the two algorithms demonstrate different growth rates.

As you can see in the output and Figure 24, when the pattern string is significantly smaller than the text, a doubling of the text size (\(n\)) basically doubles the execution time of both functions. Both algorithms grow as \(O(n)\), and the extra processing in rk_strmatch makes its implementation slightly slower.

However, when the pattern string is comparable in size with the text, Figure 25 illustrates a very different result. The rk_strmatch function starts out slightly slower than the bf_strmatch function, but as the size of both the pattern and text strings double, the rk_strmatch function experiences only a doubling in its running time. The doubling of the pattern string doesn’t affect its running time; only the doubling of the text file affects the running time, as our \(O(n)\) complexity analysis predicts. The running time of the bf_strmatch function, on the other hand, grows by approximately a factor of 4, corresponding to the doubling of both \(m\) and \(n\) and the algorithm’s \(O(n^2)\) complexity bound when \(m\) and \(n\) are comparable.

Problem unsolved. We’ve come to the end of the chapter, and we haven’t yet solved our problem: how do we make it easy to find the webpages that mention a particular word or phrase? And by easy, we’ve learned that this problem’s biggest challenge is in the time it takes to solve. While Rabin-Karp is faster than brute-force string matching, it alone isn’t fast enough to power Google search.[22] But the technical details of Rabin-Karp provide the key to running web searches quickly.

In the next chapter, we’ll explore these details and learn about a technique called hashing, which is how Rabin-Karp beats brute force. Hashing will lead us to hash tables, a widely used data structure, which just happens to be at the heart of Python’s dictionary data type and Google search. Hashing and hash tables will also introduce us to a new problem-solving approach. Onward!

---

[1]

In October of 2020, Google posted a video titled “Trillions of Questions, No Easy Answers: A (home) movie about how Google Search works” (https://www.youtube.com/watch?v=tFq6Q_muwG0&t=6s). This video is also highlighted on Google’s page describing how it thinks about search (https://www.google.com/search/howsearchworks/).

[2]

https://www.google.com/search/howsearchworks/our-approach/

[3]

https://www.ibm.com/topics/natural-language-processing

[4]

https://www.google.com/search/howsearchworks/how-search-works/organizing-information/

[5]

In Chapter 2, we saw three different approaches: membership test using the in-operator; Python’s string-find method; and our own for-loop-based string-find.

[6]

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein, Introduction to Algorithms (Cambridge, MA: The MIT Press, Third Edition, 2009), 985.

[7]

Remember that we can write any statements in our pseudocode as long as they are steps that can be carried out by a machine. Since you’re more comfortable with Python now, I’ll sometimes write pseudocode with very Python-like statements (e.g, the for-loop).

[8]

The `bf_strmatch.py` script is configured to accept the pattern `p` and text `t` in numerous ways. If you run the script without any command line parameters, it will prompt you for `t` and `p`. Or you can put both `t` and `p` (in that order) on the command line; don’t forget to put quotes around these strings. To search texts that contain newline characters, you just give the pattern on the command line. When you hit return and start running the script, it will read whatever you next type as the text-to-be-searched. You end your text with a Ctrl-D. Or you can type the `bf_strmatch` function into the interactive Python interpreter and then run the tests as shown.

[9]

We will continue to look only at different implementations of our algorithms in Python, but everywhere we ask questions like this, you should include changing the programming language as something you might choose to do differently.

[10]

We’ll see an example of such type-checking tools in Chapter 16.

[11]

On most computers, there is a standalone time utility like the one I use in the example. Your results should be similar whether you use this or others like it.

[12]

https://www.gutenberg.org/ebooks/2600

[13]

https://www.gutenberg.org/ebooks/440

[14]

We’ll talk more about the shell, `stdin`, and the redirecting of our script’s inputs and outputs in Chapter 13.

[15]

A similar line exists in `bf_strmatch2.py`.

[16]

You might have a machine faster than mine, and if so, you still may not see a difference. Using `cmp_bf_times.py` in the tip below, try even bigger inputs until you see the difference.

[17]

This calculation assumes that most of the elapsed time is spent in the for-s loop (lines 11-13). Even if I’m wrong, it will change our answer by at most a factor of 10. The conclusion that we need to find a better algorithm remains.

[18]

https://en.wikipedia.org/wiki/Rabin–Karp_algorithm

[19]

I ignore the case when the pattern string is empty because that’s a trivial result. Every shift is a valid shift when the pattern string is empty. We don’t need to run the algorithm, and we could add a conditional at the start of our functions that checks for an empty pattern string.

[20]

The other if-statement in the matching loop in `rk_strmatch` (i.e., line 51) has an execution cost proportional to 1, and we can ignore it.

[21]

I ran `python3 cmp_strmatch.py` at the shell prompt. I grabbed the output and formatted it so that it’s easier to read the results of the two tests.

[22]

Rabin-Karp is fast, but there are string-matching algorithms that are even faster. For example, the Knuth-Morris-Pratt algorithm has the same pre-processing bound as Rabin-Karp (i.e., O(m)), but a better worst-case matching bound of O(n) for all inputs. Technically, its bounds are 𝛩(m) and 𝛩(n). Yup, you need to go learn the difference between Big-O and Big-𝛩 notation!