Chapter 11: Discover Driving Directions

We began this act with a search problem that asked us to create a listing of all web pages that mention a particular keyword or phrase. Search was effectively a question of matching. Are there search problems that are more than just matching against a pattern? Google definitely thinks about search much more broadly. It searches over many different sources of digital information seeking answers to our questions.

In this chapter, we expand our definition of a search problem to include the many processes we use in our daily lives to find solutions to questions for which we have a well-described goal. We will consider several different instances of this, but one of the most recognizable examples of goal-directed search is the finding of a path from one point on a map to another.[1] You have almost certainly used this type of software in driving across the country or walking in an unfamiliar city, and how such software works is this chapter’s problem-to-be-solved.

A new approach to programming. In addition to introducing a new problem-solving technique (i.e., goal-directed search), this chapter’s problem will require us to move beyond a procedural approach to programming. To this point, we decomposed each problem into functional components and then “wired” these components together in a sequence of steps that when executed produced a solution. This approach is not that much different than the recipes we follow when cooking. And with a recipe (i.e., an algorithm), we took its functional components and separately designed them.

A procedural approach uses the power of abstraction to create a public interface that hides each function’s implementation. This is functional abstraction, and it allows us to think first about a component’s outputs in terms of its inputs, and then later worry about the set of computational steps that would turn specific inputs into the desired outputs. And when the public interface created a useful abstraction, we found that we could reuse this function across our program and hopefully other programs we or others might write.

Encapsulation is another benefit of the use of a public interface and hidden implementation. When we hide a function’s implementation, we can test, debug, and even change the function’s body without affecting the sites that call our function. By now, you know that creating a correct program is hard work and that it’s practically impossible to write a correct program in one go. But by using functional abstraction and encapsulation, we can build toward a correct program, one piece at at time. And when we miscode a component, we can fix the bugs in that component without causing a domino of changes in the rest of our program.

In sum, we use decomposition and functional abstraction to break complex problems into simpler pieces, and functional abstraction and encapsulation to code each piece separately.

While a procedural approach to programming works well, it has limits. When the objects that our scripts manipulate are ones built into Python (e.g., strings, ints, and lists) or ones provided in some module built by a Python programmer (e.g., network responses and digital images), focusing on the functions in the recipe works well. However, to solve this chapter’s problem, we are going to need to think about more than its component tasks. We are going to need to build our own objects, i.e., some of the ingredients needed in our recipe. In other words, we are going to need to build our own data abstractions.

But have no fear (said the Cat in the Hat), you already have the tools you need to build data abstractions: decomposition, abstraction, and encapsulation! When applied to data (instead of just procedures), you enter the exciting world of object-oriented programming (OOP). Python is an object-oriented programming language, which means that it contains features designed to make data abstraction easy.

By the end of this chapter, you will have gained the ability to create recipes and ingredients, which will allow you to solve an unbelievably wide range of complex, real-world problems. Computer scientists think of this pairing as algorithms and data structures. There are many elegant ideas in this space, and through the rest of this act, you’ll get a taste of the rich world of classical algorithms and data structures.[2]

Learning Outcomes

Learn to write a script for goal-directed search and to simulate what you cannot analytically solve. You will understand the difference between procedural and object-oriented programming, and you’ll build algorithms and data structures relevant to finding driving directions from a map. By the chapter’s end, you will be able to:

• Describe the components of a formal specification for a goal-directed search problem [design and CS concepts];

• Discuss the parallel nature of goal-directed search and finite state machines [design and CS concepts];

• Code a random walk across a graph-like data structure with notes and edges [programming skills];

• Argue that the random walk you coded will terminate [CS concepts];

• Simulate real-world phenomenon and discuss what you can learn from these simulations [design and CS concepts];

• Understand the benefits of object-oriented programming and how it differs from procedural programming [CS concepts];

• State the differences between a class and an instance of that class [CS concepts];

• Use classes to build your own data structures and inheritance to avoid duplicating code found in related classes [design and programming skills];

• Employ Python’s magic methods so that the objects you build look like they were built into Python [programming skills];

• Describe the purpose of Python’s self convention [programming skills];

• Discuss the importance of the representation invariant for writing robust object-oriented code [CS concepts];

• Understand how to build a data structure that represents a map and practice building your own classes [programming skills];

• Write a script that finds a solution to the driving directions problem and specialize it to perform searches with different algorithmic characteristics (i.e., breadth-first and depth-first search) [design and CS concepts];

• Describe the difference between uninformed and informed searches, and state the power (and danger) of heuristics [CS concepts].

Driving directions, a formal specification. Solving a goal-directed search problem, like the finding of directions from one point on a map to another or cooking a delicious meal, is straightforward once you understand how to model a goal-directed search problem. A good place to start in this modeling is with the problem’s start (or initial) state and its goal (or final) state. These states can be as simple as “I’m here” (start state) and “I want to be there” (goal state), or “I have these ingredients available to me” (start state) and “I want to serve a delicious dinner” (goal state).

Besides these two states, goal-directed search problems have a set of valid actions through which we can manipulate the current state. In the driving context, I have a set of roads (the valid actions) that move me from one location (the current state) to another. In the cooking context, I have a set of kitchen instruments and things I can do with them (the valid actions) that change the state of the ingredients.

The many road locations and partially prepared mixtures of ingredients are states, along with our designated start and goal states, that exist in the problem’s complete search space. We might be able to enumerate all these states for a particular goal-directed search problem, but in real applications, we don’t often try. All that matters is that we can distinguish one unique state from another, which is, once again, an encoding problem that translates a collection of real-world things into a computational form.

The solution to a goal-directed search problem is a finite sequence of valid actions that when performed will transform the start state into the goal state. If we cannot find such a sequence, then there is no solution to the problem (e.g., there are no roads that take you from your starting location to your desired goal location).

Parallels with finite state machines. Does this model description remind you of a finite state machine (FSM), which we discussed in Chapter 2? It should! We drew a FSM as a model with nodes, which captured their current state information, and directed arrows (also called edges) between these nodes, which were the allowable actions that changed the state represented by the node at the arrow’s tail to that represented by the node at the arrow’s head. The same is true in a goal-directed search model.

While both models have a single start state, they may differ in their number of goal states. You’ll recall that a FSM may have one or more goal states, which together cover the set of valid input strings. In goal-directed search, we typically have a single goal state.

To understand importance of this difference, you need to remember the purpose of each model. A FSM distinguishes valid strings from invalid ones. These strings are input to the FSM, and they drive the sequence of steps taken by it. At the end of the input string, the FSM reports whether the sequence ended in a goal state.

In goal-directed search, the sequence of steps is not being driven by some external input. Instead, it is the job of our script to search for some sequence of steps that takes us from the start state to the goal state. If in this search, our code ever hits the goal state, it stops and reports the sequence of steps it found that moved it from the start state to this goal state.

This fundamental difference in purpose is one of the reasons why we talk about the set of all states in a FSM and yet say that we’re not often concerned with the full enumeration of states in a goal-directed search problem. In a FSM, when the input veers off a known path toward a goal state, our script can raise an error. In goal-directed search, we don’t know what sequences of steps lead us to the goal state until we find one, and when we find one, we may be uninterested in finding another.

Solutions with specific characteristics. In goal-directed search, there is a lot we don’t know. First, we don’t know, given a particular set of nodes and edges, if it is possible to get from the start state to the goal state. And when there is a solution, we don’t know if there is more than one.

Sometimes, all we care about is finding a solution (or reporting that there isn’t one), and any will do just fine. For example, any road that gets me home is a good road. Other times, we may decide to put some constraints on the search problem so that it yields solutions with specific characteristics. For instance, we may not feel that all roads are equally desirable: If we can get home without taking a toll road, that’s what we’d like. A solution with the desired characteristics might not exist, but if one does, our script should return it.

Let’s walk before we drive. Let’s stop talking about what a script that implements goal-directed search should do and start building one. The first thing we need for our problem-to-be-solved is a city map. We can build a nice regular one with the abstract data type CitySqGrid.[3] We simply tell it how big we would like our square grid of city blocks to be.[4]

from city import CitySqGrid

not_Boston = CitySqGrid(4)
print(not_Boston)

You’ll notice that the constructed CitySqGrid object places an s at the city center, which is the starting point for our journey. As for the goal state, let’s imagine that this city is surrounded by a countryside of open fields, and we’d like to spend our day relaxing in one of these fields and playing with my dog. We don’t care which field; we simply want out of the city for the day.

The abstract data type CitySqGrid has an attribute that we can use to grab the coordinates of the starting location (CitySqGrid.start), which will be the initial value of this search problem’s current state. Starting there, the loop on lines 13-16 in the code block below allows us to walk Cosmo around the city until we hit our goal state (i.e., until the current state loc is outside the city). CitySqGrid has a method called move that makes it easy to step 'north', 'south', 'east', or 'west'.[5] The method takes our current location (i.e., the current state) and a direction, and it returns a location that becomes our new current state. By the way, in the code block below, we tell CitySqGrid that we want our location on the map to look like my dog Cosmo rather than the boring s character.[6]

### chap11/walk.py
from city import CitySqGrid

# Our faithful dog
Cosmo = '\N{DOG FACE}'

# Build the city and put Cosmo at its center
nyc = CitySqGrid(4, Cosmo)
print(nyc)

# Loop that walks Cosmo
loc = nyc.start
while loc in nyc:
    direction = input('Where to? ')
    loc = nyc.move(loc, direction)
    print(nyc)

print('Enjoy your day outside the city!')

When we walk Cosmo around this virtual city, move won’t let us walk into a building. Since we don’t live in these buildings, we are not allowed in. What this means is that the CitySqGrid data type is smart enough to know that we can walk only on the streets and not off them. This is important if we want to successfully build a set of driving directions that won’t have our car driving through buildings and fields.

A random walk. Notice that the script walk.py handles a piece of this chapter’s problem: it alerts us when we have reached the goal state (i.e., our walk took us out of the city). What it doesn’t do, without our active help, is search the city for a route to this goal state.

How might we think about a procedure that would get us from the city center to the fields on the outskirts of the city? And for this question, let’s assume that we don’t know anything about the layout of the city except what we see immediately around us. If you’ve spent any time solving mazes as a kid, you probably can think up several different techniques that might work. I’m going to suggest we have the script do the easiest thing possible: for each step the script takes, it randomly chooses a direction.

This is easy to code, as we’ll do in a moment, but first let’s ask: Will a random walk reliably get us out of a city? The answer to this question should be yes. In fact, for any of the techniques you were just imagining, we want the answer to be yes. If not, then there are some maps on which the technique won’t work, and that’s bad if we assured someone that we had a script that always finds a route when one exists.

What we’re talking about here is the proof of correctness we mentioned as one of the three formal components of an algorithm. Again, this book doesn’t teach you how to create a formal proof of correctness, but we can make a stab at the form of the proof for a random walk.

Will it work? To argue that a random walk will get from the start state to the goal state if a path exists, we might begin by thinking about every type of city layout imaginable, and then test our approach against that infinite set of layouts. Yes, that sounds hard and is probably impossible to do.

So instead, good theoreticians and problem solvers transform these hard questions into their equivalent inverse. For us, this means we need to answer the question: What would need to be true to not allow a random walk to find the goal? If we can rigorously argue that there is nothing keeping us from finding a solution, then we can confidently state that a random walk will reliably get us out of any city.

The argument is fairly simple. We begin by eliminating the case where there is no path from the start to the goal state. Clearly a random walk would fail in this case; however, no procedure would find a path that doesn’t exist. As such, the real question is: Is it possible for a random walk to never find a solution path when one exists? The answer to this question is no. If a solution path exists and our algorithm can generate that path, there is some probability that it will randomly generate this sequence of steps and achieve our goal.

A short walk, please. The kicker is, how long might we have to wait for a script that implements a random walk to find a sequence of steps that end in the goal state? Hard to say, right?

Let’s again transform the question. What structure in a map might make it take an unbounded amount of time to find the solution? The answer might have popped into your mind. A loop!

In reality, we don’t even need a loop in the roads to have a situation where our random walk takes forever. The algorithm might repeatedly generate a step west followed by a step east, and then west, then east, west, east, …. Even in a city with a single road that leads from the city center to a field on the outskirts, this possible sequence of steps would cause our algorithm to never return.

No loops. We can eliminate solutions that take a really large amount of time (and space) to generate by eliminating loops from our search space.

Fig. 30 Starting in the center of the city and then following the 8-step path 'eennwwss' puts us exactly back where we started. We can remove any such loops from the space of paths we should search because they don’t advance us toward our goal.

For example, a solution that heads straight east in our city with a square grid is a solution to our problem. One that heads straight east, but loops around the first block one time before continuing to proceed east, is another solution. However, the first 8 steps of the sequence 'eennwwsseeee' put us directly where the sequence 'eeee' also starts (i.e., the start state, as illustrated in Figure 30). If an algorithm has already explored a path that starts at the current state and returns to that state, repeating this path clearly won’t advance us toward a solution. This means that we can eliminate loops in our maps and not worry that we will miss finding a solution.

Only visit new spots. A necessary condition of looping is that we must visit the same location more than once. If we create a random walk algorithm that is not allowed to visit a location more than once, we can guarantee that the algorithm will either find a (loop-free) solution or get caught in a “dead-end.” A walk ends in a dead-end if the algorithm cannot find a new location to visit from its current location. For example, in our previous example, the first 8 steps of the sequence (i.e., 'eennwwss') leaves us without a valid location to visit next that hasn’t already been visited.

If you think about it, no run of this algorithm will take more steps than there are locations in the map. It may still take many random walks to find a solution, but no single random walk will take infinite time.

A dog walk. Let’s implement this random-walk algorithm, and since my dog Cosmo is much better at a random walk than I am, we will simulate him wandering around a city. His nose will tell him if he is about to repeat a location he’s already visited, which will guarantee that our algorithm doesn’t fall into any wasteful loops. The function dogwalk in dogwalk.py implements this behavior.

You Try It

Run python3 dogwalk.py. The first printing of the city displays Cosmo at the start position. The second illustrates the random path he took (i.e., the asterisk characters mark the path[7]). Run it several times until you’ve seen that he can get both outside the city and caught in a dead end.

### chap11/dogwalk.py
from city import CitySqGrid
import random

# Our faithful dog and the scent he smells
Cosmo = '\N{DOG FACE}'
EXPLORED = '\033[34m*\033[0m' # blue *

def dogwalk(my_city):
    """Given a city of type CitySqGrid, take a random walk
       and return True if goal successfully met. The
       successful path is marked in the city object."""
    # Set the current state
    cur_loc = my_city.start
    
    while cur_loc in my_city:
        # Where to? Well, what steps are possible?
        moves = my_city.possible_moves(cur_loc, EXPLORED)
        # print(f'DEBUG: cur_loc = {cur_loc}; moves = {moves}')
        
        if len(moves) == 0:
            return False   # dead end!
        
        # Randomly pick a possible move and make it
        a_move = random.choice(moves)
        next_loc = my_city.move(cur_loc, a_move)
        
        # Leave a scent at current loc
        my_city.mark(cur_loc, EXPLORED)
        
        # Update current state
        cur_loc = next_loc
    
    # The random path was successful!
    return True

Terminology

It is worth reviewing the terminology I mentioned in Chapter 1. In the function dogwalk, my_city is an object, and this object has a set of attributes associated with it. For example, the attribute start is a data attribute (i.e., it names a data object) and the attributes possible_moves, move, and mark are function attributes (also called methods that we call like a function).

The algorithm in the function dogwalk builds upon that in walk.py. It sets the current state (i.e., cur_loc) to the starting location in the city, and then it falls into a while-loop that iterates until this current state matches our goal. Inside the loop, we call my_city.possible_moves, which returns the list of possible moves we can make from our current location. This method’s second argument is the character we use to mark already-visited locations in the city; these marks are made on line 29. With a valid list of possible moves, the algorithm randomly picks one and moves there (lines 25-26). Of course, it can make a move only if Cosmo isn’t at a dead end, which is the check on lines 21-22. Finally, line 32 prepares the algorithm to repeat these actions with the new location where Cosmo moved.

Here’s the main function in dogwalk.py that builds a small, regular city and then has Cosmo go for a walk.

### chap11/dogwalk.py
def main():
print('\nBuilding a city with a 4x4 square grid')
    nyc = CitySqGrid(4, Cosmo)
    print(nyc)
    
    # Cosmo walks himself
    success = dogwalk(nyc)
    print(nyc)
    if success:
        print(f'Cosmo is frolicking in the fields!')
    else:
        print(f'Cosmo hit a dead-end.')

The algorithm in dogwalk illustrates the core of goal-directed search. It’s not quite the algorithm we want for our driving directions problem, since it gets caught in dead ends when there exist valid paths from the start location to the goal location. We’ll fix this issue later in this chapter. But first, I want to show you how to use dogwalk to reveal interesting facts about our physical world.

Simulation. Consider this question: When Cosmo takes himself on a walk, how likely are we to find him wandering around in the fields versus stuck somewhere in the city? Using dogwalk, we can learn that the answer to this question depends upon the size of the city. We simply review the outcomes of many random walks, and this empirical process gets us an idea of a likelihood.

Let’s implement this. The next code block builds a self-avoiding random walk simulation from dogwalk.py’s main routine.[8] You tell the sim function how big to make the city and how many trials to run. With a CitySqGrid object of the specified size, the function repeatedly[9] invokes dogwalk and keeps track of how many of times Cosmo hit a dead end. When the number of trials is complete, it computes the percentage of dead-end runs.

### chap11/sim.py
from city import CitySqGrid
from dogwalk import dogwalk, Cosmo

def sim(blocks, trials, verbose):
    # Initialize the metric of interest
    dead_ends = 0
    
    # Build the specified city
    my_city = CitySqGrid(blocks, Cosmo)
    if verbose:
        print(f'\nBuilding a {blocks}x{blocks} city')
        print(my_city)
    
    for _ in range(trials):
        # Reset the city before each trial
        my_city.reset()
        
        # Run, record, and print the trial
        success = dogwalk(my_city)
        if not success:
            dead_ends += 1
        if verbose:
            print(my_city)
    
    # Print the percentage of trials ending in dead ends
    print(f'{100 * dead_ends // trials}% dead ends')

You Try It

1. Run sim.py several times with a block size of 4 and trials equal to 20 (i.e., run python3 sim.py 4 20. It’ll probably report that approximately 5-15 percent of Cosmo’s walks ended in a dead end.

2. Now double the size of the city and run the simulation several times again. This time it’ll probably report that 25-40 percent ended in a dead end.

3. Finally, double the city size once more. The likelihood of a walk ending in a dead end has jumped again, to somewhere around 80-90 percent.

Our conclusion: In a small city, we should look for Cosmo in the fields; in a big city, he’s probably still somewhere inside it. This simulation taught us a fact about our world.

A self-avoiding random walk is used to simulate an aspect of the world that no one knows how to model analytically. It is an important simulation technique in numerous areas of math, science, and engineering. It helps, for example, biologists learn about the topological behavior of proteins, which is an important challenge without an analytical solution.

To maps through OO programming. Let’s return to our driving directions problem. In addition to the problem that dogwalk.py may print a path that’s a dead end, this script works with regular city grids. We want it to produce driving directions for any roadmap. In other words, we need a data type that is more general than what we have with CitySqGrid. Where can we find such a data type? Well, where did this CitySqGrid data type come from?

The answer is that I built it. You won’t find CitySqGrid in the Python language documentation or in a Python module that some generous soul published. Was it obvious to you at any point that it was something I wrote? Hopefully not, and this is the beauty of coding in a well-designed, object-oriented language. We’ve been using instances (e.g., my_city) of CitySqGrid, and as long as we understood its interface and behavior (i.e., its abstraction), we happily used it to solve our problem as if the data type was a part of Python.

This is power of object-oriented (OO) programming, which uses data abstractions as well as procedural abstractions to simplify problem solving. With a facility to create data abstractions, we are freed from using just the data types that Python or some Python library provides.

Tip

At first, OO programming may feel overwhelming as it comes with a boatload of syntax and jargon. Even I find the OO terminology to be intimidating and confusing. But there’s nothing to fear here as you have been using the OO approach from this book’s start. Everything you manipulate in Python is an object, even what feels primitive and simple, like integers and strings. I’ll introduce you to the basics of OO programming, and if you’d like to learn more, you might next read Chapter 10 in John Guttag’s book titled an Introduction to Computation and Programming Using Python.[10]

Classes. If you look at line 4 in the module city.py, you’ll see the following:

### chap11/city.py
class CitySqGrid(maze.Maze):

This is the class definition for CitySqGrid, and classes are how we implement data abstraction in Python. In other words, through the Python keyword class, you define and implement new data types. In a bit, I’ll explain what goes in the parentheses when you define a new data type.

Like a function definition, a class definition defines a data type’s interface and makes explicit its implementation. When we learned about functions and their definitions in Chapter 3, it was easy to identify the public interface from the private implementation. The same separation exists with classes, but it is harder to see, especially in Python.[11] If your new data type is anything but trivial, it becomes very hard to understand how to use it by simply reading the class’s definition. This means that docstrings and comments become extremely important.

Tip

I have described the interface for CitySqGrid (i.e., its abstraction as seen through its data attributes and methods) in a docstring at the top of its class definition. I further adopt the convention of following the docstring with a comment that is meant not to help users of the data type but those who want to modify its implementation. Follow this convention or imagine your own—just give those who will use your data type some clear way to understand what’s in its interface and what are implementation details.

While I’ll continue to make reference to the CitySqGrid class, it is too complicated to use as an understandable first example. Instead, I’ll teach you how to build your own class by creating a new data type, called Pin, that allows us to add Google-Maps-like pins[12] to the CitySqGrid maps we used in walk.py.

### chap11/pin.py
class Pin(object):
    """Abstraction: A Pin object is a mark at a map location `loc`
       with a `name`, descriptive `note`, and a ranking of 0-5 `stars`.
       These names are all instance attributes.

       instance.icon: The pins displayed icon, which depends upon
       the pin's number of `stars`.

       distance(location): Given a (x,y) location, this method
       computes and returns the as-the-crow-flies distance from it
       this pin's location, but only if this pin is highly rated.

       __str__(): Converts the pin into a string.
    """
    # ... implementation of the Pin class follows ...

You Try It

In the chapter’s GitHub repository, you’ll find the script wander.py, which adds pins to the functionality of walk.py. Run python3 wander.py and it will print a 6x6 square city with pins and Cosmo ready for his walk. The pins are the green hearts and red x-marks on buildings. Walk Cosmo around the city as you did in walk.py, or type a c to teleport him to the nearest green heart (i.e., one of his highly-rated places). If you type a q or step outside the city, your wanderings come to an end.

Building an instance. The function main in wander.py builds a list of pins (lines 68-73) and then iterates over this list to mark the pin locations in the city it built (lines 65 and 74-75).

### chap11/wander.py
def main():
    # Build the city and put Cosmo at its center
    nyc = CitySqGrid(6, Cosmo)
    
    # Add Cosmo's favorite pins to the city map
    pins = [
        Pin((3,11), "Park", "Lots of squirrels", 5),
        Pin((7,9), "Fire Hydrant", "Many good smells", 4),
        Pin((5,3), "Cat", "Not a nice cat!", 1),
        Pin((9,1), "Bakery", "Free dog treats!", 5)
    ]
    for pin in pins:
        nyc.mark(pin.loc, pin.icon)
    
    print(nyc)
    
    wander(nyc, pins)
    
    print('Thanks for the fun walk!')

Line 69 creates an object (also called an instance) of type Pin. If you think about Python’s built-in data types, like integers, strings, and lists, there is special syntax in the language to handle the creation of objects of these types. For example, when we type a number without a decimal point, the Python interpreter knows we want to create an integer object with that number as its value. For strings, we put the value in a matching pair of quote characters. For lists, we use square brackets.

# Examples of creating an instance of a built-in object. We get to use special
# syntax in each of these cases.
an_int = 0
an_empty_string = ''
an_empty_list = []
print(an_int, an_empty_string, an_empty_list)

But we can also build instances of these built-in data types by directly invoking their constructors. The form of a constructor is the class name (i.e., its type) followed by a pair of parentheses. The result of a call to a constructor is a newly minted object of that type.

# The same examples as the last code block, except now we're creating
# instance of built-in object using the type's constructor.
an_int = int()           # constructor defaults to an object of value 0
an_empty_string = str()  # constructor default is an empty string
an_empty_list = list()   # constructor default is an empty list
print(an_int, an_empty_string, an_empty_list)

It is possible to initialize these objects to values other than their defaults by passing in an initialization value in the constructor call.

# With some initialization values
an_int = int(0)
a_string = str(an_int)
a_list = list(a_string)
print(an_int, a_string, a_list)

This constructor syntax is how I created, in wander.py on line 65, a 6x6 instance of CitySqGrid with a dog-face character at its center (named nyc). It is also how I created a Pin object on line 69.

This creation takes two steps. First, the interpreter grabs a raw piece of our computer’s memory that’s large enough to hold all the instance’s attributes (i.e., all the data specific to this object). By raw, I mean that none of this memory is initialized in such a manner that object acts like an instance of CitySqGrid or Pin. Initialization, the second step, is the job of a class’s __init__ method.[13]

### chap11/pin.py
    def __init__(self, loc, name, note, stars):
        self.loc = loc
        self.name = name
        self.note = note
        
        assert stars >= 0 and stars <= 5, "Invalid number of stars"
        self.stars = stars
        
        if self.stars >= 3:
            self.icon = green_heart
        else:
            self.icon = red_x

An __init__ constructor is just a function defined in a class’s namespace[14] (i.e., you indent it under the class definition). Comparing line 23 above with lines 69-72 in wander.py at the start of this section, the Pin constructor’s last four formal parameters match the four actual parameters provided in the constructor call. Unexpectedly, the interface definition also includes the name self as the function’s first formal parameter.

Self and instance attributes. Every method definition must contain this additional formal parameter called self[15] (and it must be listed first). The self parameter gives you a way to distinguish data attributes belonging to an instance (called instance attributes) from those shared across all instances (called class attributes). When we call the Pin constructor on line 69, it returns a Pin object with location (3,11), name "Park", and so forth. The constructor stores the first two parameter values in the two instance attributes self.loc and self.name (on lines 24 and 25 of pin.py). These values[16] take up memory space in the Pin object that is the first element of the pins list. The Pin object in the list’s second element has different values for its instance attributes.

Although we won’t use them in this book, you can also create class attributes (also called class variables). With a class variable, you don’t have that variable for each instance, but a single variable that is shared by every instance of the class. If, for example, the name note was a class variable, you’d write Pin.note rather than self.note in a class method (i.e., you replace self with the class name as the namespace).[17]

Finally, be careful not to confuse instance variables with local variables. The name loc in Pin.__init__ is a local variable. If you look at the implementation of CitySqGrid.__init__, you’ll see that I create the local variable row1 to name an intermediate computation. These local names exist only while the method is running. Instance variables, on the other hand, are names with values that we want to persist between method executions.

Tip

Knowing whether you need to prepend self to a name is tricky, and it will take some time for you to naturally know when and when not to use it. Until you do, I suggest you pause as you write a variable name in a class method and ask yourself, “Am I trying to access an attribute of a particular instance of this abstract data type (i.e., class), or is this just a local variable that is helping me to complete the work of this method?” You need self in the first case, and not in the second.

As you can see in the function body of Pin.__init__ (lines 24-34), instance variables are sprinkled throughout the constructor’s implementation. If you explain your data type’s abstraction in a docstring, a user won’t have to read through your constructor to try to understand what attributes you’ve made available.

Methods. In addition to __init__, the class definition in pin.py defines two other methods. The distance method computes the as-the-crow-flies distance between the instance variable self.loc and the method’s formal parameter loc. I use this method in wander.py (line 41) to have Cosmo jump from his current location in my_city to the closest, highly rated pin.

### chap11/pin.py
    def distance(self, loc):
        if self.stars >= 3:
            return abs(math.dist(self.loc,loc))
        else:
            return MAX_DISTANCE

### chap11/wander.py
        elif cmd == 'c':
            best_loc = NO_LOC            # not a valid location
            best_distance = MAX_DISTANCE # bigger than any allowable map
            
            # Find the closest highly-rated pin
            for pin in pins:
                dist = pin.distance(cur_loc)
                if dist < best_distance:
                    best_loc = pin.loc
                    best_distance = dist
            
            assert best_loc != NO_LOC, "Failed to find a pin"
            
            # Teleport to within one step, which requires me to erase
            # the character from the cur_loc.
            character = my_city.get_mark(cur_loc)
            my_city.mark(cur_loc, ' ')
            cur_loc = (best_loc[0] - 1, best_loc[1] - 1)
            my_city.mark(cur_loc, character)
            direction = 'n'

The method distance could have been a function outside the namespace of the class Pin, but in OO programming, your goal is to put functions that operate on a class’s instances in the class definition. In this way, the class definition bundles together the data (as attributes) and functions (as methods) that work together on a particular abstraction (i.e., maps and pins in our running examples). This bundling (called encapsulation) helps you (the class designer) make sure that a class’s data are properly managed, as I explain further in the next section. As the scripts you write grow in size, you’ll also find that this encapsulation helps to organize your code in a manner that makes it easier to understand and maintain.

Representation invariant. As we model the world in our scripts, we’re not just manipulating data but trying to build useful abstractions. In a class, the __init__ method is not only responsible for initializing a new instance but also for creating a valid representation of a class’s object. For example, our pins have a star rating, and this rating should be between 0 and 5 inclusive. The Pin.__init__ method contains code (lines 28-29) that guarantees a new Pin object adheres to this representation invariant.

While the __init__ method establishes the representation invariant, the other class methods are expected to maintain it. The Pin.distance method does because it doesn’t change any of the instance variables. A more interesting example is CitySqGrid.reset, which makes sure when we reset a CitySqGrid object back to its initial state that we put the character (e.g., the Cosmo dog emoji) back at the grid’s center (see line 67 in city.py).

Ensuring that your class’s methods never break the representation invariant is one goal, but you should also design your class so that its users aren’t able to break it. My Pin class does not fully protect its representation invariant because a user could write a value to a_pin_object.stars outside the expected range. We could fix this problem by following the setters and getters pattern in OO programming, which gives the class designer control of a user’s access to the class’s attributes.[18]

Magic methods. The last undiscussed method in the Pin class is __str__. Like __init__ and unlike distance, this method’s name starts and ends with two underscore characters. Methods that start and end with two underscores are called magic methods in Python, and they are what allow you to treat an instance of your class just like Python’s own built-in types.[19]

### chap11/pin.py
    def __str__(self):
        return f"{self.name} at {self.loc} rated {self.stars}" + '\u2605'

The method __str__ should always return a string. As the data type’s designer, I can return any string I like, and I’ve chosen to return a simple description of the Pin object using a few of its attributes. This is a magic method because the interpreter looks for it when a Pin object is used where the interpreter expects a string object. For example, the input parameters to print are expected to be strings, and when we pass a Pin object as a parameter to print, the Python interpreter looks for this specific magic method and, if it finds it, it uses it. The main function in pin.py runs a few tests on the Pin class and uses CitySqGrid along the way; it demonstrates how easy a __str__ method makes printing the instances of classes we define.

### chap11/pin.py
def main():
    # Our faithful dog
    Cosmo = '\N{DOG FACE}'
    
    # Build a city
    nyc = CitySqGrid(6, Cosmo)
    
    # Create some pins and keep track of them in a list
    pins = [
        Pin((3,11), "Park", "Lots of squirrels", 5),
        Pin((7,9), "Fire Hydrant", "Many good smells", 4),
        Pin((5,3), "Cat", "Not a nice cat!", 1),
    ]
    
    # Add each pin in pins to the city map
    for pin in pins:
        print(f'Adding {pin}')
        nyc.mark(pin.loc, pin.icon)
    
    print(nyc)

You Try It

Use the dir command to see what attributes are in the list namespace, i.e., dir(list). You’ll find __str__. Now you know how we’ve been able to print so many Python objects by just passing them as parameters to print.

The docstring on CitySqGrid describes several other magic methods that we’ve used. For example, the __contains__ method allows us to use the Python operator in with a CitySqGrid. This method requires a parameter, which is a location in the city grid we’re asking about. It becomes the value to the left of the in operator and the CitySqGrid instance we want to check is to the right. In other words, the Python interpreter changes the second code block below into the first one.

loc = (1, 1)
nyc.__contains__(loc)

loc = (1, 1)
loc in nyc

The key idea here is that, when we define our own data type, we want to use it like those built into Python.

Tip

Implement as many of the Python magic methods as make sense for your class. It will make it easier for you and others to use your data type.

Building on others. It’s finally time to explain what’s in the parentheses on the class definition line. The Pin class definition begins with class Pin(object) and CitySqGrid with class CitySqGrid(maze.Maze). I built both these data types, but I didn’t design them from scratch. I built each as a specialized kind of a more general data type. This more general data type is what you put in the parentheses of the class definition.

The Pin class builds on a class called object, which is a class at the root of the Python object hierarchy. Every object of a built-in Python data type is also an object of type object. By saying that Pin is derived from object, I’m saying that I want Pin objects to be Python objects. Similarly, every instance of CitySqGrid is an instance of the data type called Maze, which is itself an instance of object (as seen in maze.py). Object-oriented enthusiasts call CitySqGrid a subclass of Maze. As a subclass, CitySqGrid inherits the attributes of Maze.

Terminology

Along with the term subclass, you will hear the complementary term superclass. Maze is the superclass of CitySqGrid, and it shares its attributes with all its subclasses.

It’s good that a subclass inherits the attributes of its superclass because, if you look in city.py at CitySqGrid’s class definition, you’ll find only two method definitions: __init__ and reset. This is despite the fact that CitySqGrid objects use many other methods (e.g., in wander.py we used mark, get_mark, __str__, and __contains__).

The maze class is quite long, and I don’t expect you to read through it in detail. But you should understand what it means when you see some methods (e.g., __str__) in the superclass (e.g., Maze) but not the subclass (e.g., CitySqGrid). It means that objects the subclass act just like objects of the superclass for the purposes of these methods. For example, converting a CitySqGrid object into a string follows the same procedure as converting a Maze object into one.

There are only two methods in CitySqGrid that override the similarly named methods in Maze. These CitySqGrid methods exist because they need to do something different for CitySqGrid objects than what their namesakes in Maze do. Take CitySqGrid.reset; it wants to do everything in Maze.reset (as seen on line 64) plus the positioning of the character at the start location (line 67).

### chap11/city.py
    def reset(self):
        """Resets all cell contents to their original state"""
        maze.Maze.reset(self)
        
        # Reset the start point with our character
        self.mark(self.start, self.character)

In general, it’s fine for a superclass method to operate on instances of a subclass if the methods maintain the subclass’s representation invariant. If they don’t, then you should override them by redefining those methods in the subclass.

Terminology

You will find methods in the Maze class with names that start with a double underscore but do not end with them. By convention, these are helper functions. OO programming not only encapsulates the attributes and methods of a data type in a class statement, but it allows you to use all the helpful aspects of procedural programming within this statement. For example, turning a Maze object into its ASCII image involves a row-by-row generation of ASCII characters. It is easier to implement this procedure by factoring out the work done for each row into a method called __str_row and then having __str__ repeatedly call this helper function. However, this is an implementation detail, and I want it hidden from those using the data type. In Python, this hiding is done with a naming convention; other programming languages have keyword mechanisms for making certain attributes of a class private to the implementation of the class. If a piece of Python code outside the class definition calls a double-underscore-leading method at runtime, the Python3 interpreter will raise an AttributeError.

General maps. The Maze class is the abstract data type we need to build a general map and on which we’ll design a goal-directed search algorithm that produces driving directions. We’re familiar with its interface from working with CitySqGrid objects. The map I’ll use in my examples is specified by the two configuration strings: MAZE_map and MAZE_map_endpts, which are defined in maze.py. When printed, these strings produce the map in Figure 31.[20]

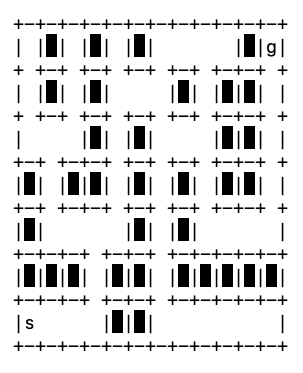
Fig. 31 The map produced by the configuration strings MAZE_map and MAZE_map_endpts in maze.py. We’ll start at the location marked with an s and follow the roads which are the empty squares. Our goal is the square with the g.

Keeping track. Now that we have a digital representation of a map and an interface that allows us to move around it, we can finally write the script that will find a set of driving directions from our start location (s) to our goal location (g). This function will do much of what the function dogwalk.py did and so we’ll start with it. However, when we ask for driving directions, we’re not interested in seeing every path that the code explores and especially not the paths that end in dead-ends. Our problem specification says that our script should execute until it finds a solution or determines that there is no path from start to goal. If you like solving printed mazes, you already know how to do this: our function will need to keep track of the parts of the map it has explored and those places on the map it can reach from start but hasn’t yet explored. By tracking these unexplored places, our script can restart its search at one of them when its current search path ends in a dead-end. And it will know that the map does not contain a route from start to goal if it ever gets to a point when it hasn’t found the goal and there are no unexplored locations left.

The function search in directions0.py implements this algorithm, starting with the frame of dogwalk. You’ll recognize the initialization of the start location (line 10) and the while-loop that continues until it hits the goal location (line 16). In the loop, it gathers possible next steps from the current location (line 18) and selects one (line 38). If there is no possible next step, it reports that there’s no path from start to goal to be found in the input map (lines 33-35).

### chap11/directions0.py
import maze

# Marks for map, which use color codes for terminal printing
EXPLORED = '\033[34m*\033[0m' # blue *
FRONTIER = '\033[32mf\033[0m' # green f

def search(my_map):
    # Set the current state and mark the map location explored
    cur_loc = my_map.start
    my_map.mark(cur_loc, EXPLORED)
    
    # Build a list on which to keep known but unexplored locations
    frontier = []
    
    while cur_loc != my_map.goal:    # search loop
        # What unexplored next steps are possible?
        moves = my_map.possible_moves(cur_loc, EXPLORED)
        
        # Add moves not already on the frontier to the frontier
        for a_move in moves:
            loc = my_map.simulate_move(cur_loc, a_move)
            if loc not in frontier:
                frontier.append(loc)
                my_map.mark(loc, FRONTIER)
        
        # DEBUG: Uncomment to watch the frontier grow
        # print(my_map)
        # print(f'DEBUG: cur_loc = {cur_loc}; moves = {moves}')
        # print(f'frontier = {frontier}')
        # input('Ready to move on? ')
        
        if len(frontier) == 0:
            print('No solution')
            return
        
        # Choose a location from the frontier as next to explore
        next_loc = frontier.pop()
        my_map.mark(next_loc, EXPLORED)
        
        # Update current state
        cur_loc = next_loc
    
    print('Found a solution')
    my_map.print()
    return

The new bit is the addition of a frontier list (line 14), which keeps track of the possible moves not yet chosen (line 24). Remember that the function dogwalk threw these other possibilities away. We now keep them so that the function ends when there truly are no other possible paths to explore (line 33).

There is one tricky aspect to the maintenance of the frontier list: we might get to a location along multiple paths from the start location (see Figure 32 for such an example). We should add such locations to our frontier list only once. Line 23 in directions0.py ensures that the algorithm abides by this condition.

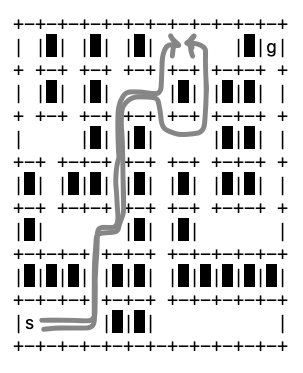
Fig. 32 Two paths from start that reach location (1,8). Our script should add this location to the frontier list only once.

You might also notice that we pop an unexplored location off the frontier list (line 38) instead of using random.choice as we did in dogwalk. You can think of this pop as making a random choice because we aren’t paying attention to what’s at the end of list. Later in this chapter, I’ll explain how a different choice affects the running of the search.

You Try It

Uncomment lines 28-31 and then run python3 directions0.py. In each loop iteration, it pauses and prints the map so that you can watch the algorithm explore the map and manage the frontier. Hit enter when you want the algorithm to continue. When you’re done, re-comment these lines and re-run the script.

Remembering how we got there. Our function search finds a path in my_map from the start location to the goal location, but this path is lost in the sea of paths that ended in dead ends. We need to add functionality to our algorithm that lets it pull this desired path out from the others. The challenge in this is that we won’t know which steps are in the desired path until search encounters the goal. Until that point, we must have it must record the actions from all its explorations. Visually, search needs to record the actions it took along the six gray paths in Figure 33, which didn’t reach the goal, as well as the single black path, which did.

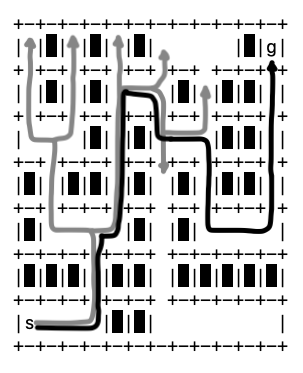
Fig. 33 The seven paths explored during the execution of search on our example map.

Tip

Recording paths like these (i.e., moving from one state to another by taking some action) is a pattern that you’ll see in many computational problems.

We record these paths by building a data structure that mimics the tree-like structure you see in Figure 33. In this figure, all paths take the same first five actions (i.e., go east three steps then north two). At location (4,3), two of the gray paths head west and the rest of the paths, including our desired black one, head east. These first five actions represent the trunk of an imagined tree, and location (4,3) represents the first branching of the tree.

We can digitally represent this tree by connecting together a series of notes to ourselves, each of which we’ll call a TreeNote. In these notes, the search function will record (at least):

1. a state (in our problem this is a map location); and

2. the action (i.e., a driving direction) taken by our search function that is connected to the recorded state.

I cryptically described the noted action because we have a choice: Do we want to record the action search took from the state in the note, or would it be better to record the action search took to get to that state? Well, which do we need to solve the problem in front of us? Which will help distinguish the black path from the gray ones in Figure 33? To answer this question, think about what you want to know when search finds the goal.

There’s nowhere to go from the goal, since search has found where we wanted to go, but it needs to know how it got there. So it needs to record the previous action that got it to the current location. And to walk all the way back from goal to start, it will want a chain of notes it can follow. Using Python classes, the data structure I’m describing would look as follows:

### chap11/directions-dfs.py
class TreeNote():
    def __init__(self, state, parent, action):
        self.state = state    # current location 
        self.parent = parent  # previous note in path
        self.action = action  # action that got us to this location

As an example of this chaining, the search function would start by creating a note for the start location, which it creates by calling the TreeNote constructor with parameters that say there is no parent note and no action that got us to start, i.e., TreeNote((1,1), None, None). From start, the only move to make in our example map is east, and the constructor call for the next location is: TreeNote((2,1), ???, 'east'), where I’ve left the parent parameter unspecified. What is it supposed to be? Right! The note (i.e., the name of the TreeNote) created at start. With the proceeding note in our current note, we’ll be able to find the location that preceded the goal. And from it the location before it, all the way back to the start.

Interestingly, branching points present no difficulties when proceeding in a tree from a leaf (i.e., the arrow heads in Figure 33) to the root (i.e., the start location). A branching location is the parent to all paths that emanate from this point. This means, if we start at the end of the black path (i.e., the goal), search can easily follow the notes it created directly back to start, and to produce driving directions, it simply reverses the list of actions it encounters as it visits each parent from goal to start.

You Try It

Don’t just read about the data structure the next script (directions-dfs.py) builds with instances of TreeNote, uncomment the debugging statements on lines 37-41, watch each step of the search, and draw your own picture of the TreeNote objects that are created and how they are linked together.

The solution. We have all the components needed to solve our problem, and we just have to implement them. Once we’ve defined our TreeNote class, we use it where needed. For example, in directions0.py, we stored unexplored map locations in the frontier list, but now when we pop from this list, we are going to want to have access to the TreeNote that goes with it. It is needed to build the notes for the unexplored locations reachable from that TreeNote’s location. If you think about this for a bit, you’ll realize that we’ll want to store TreeNote objects on the frontier list. A complete solution for search is shown below.

### chap11/directions-dfs.py
import maze

# Marks for map, which use color codes for terminal printing
EXPLORED = '\033[34m*\033[0m' # blue *
FRONTIER = '\033[32mf\033[0m' # green f

# Keep track of the tree of explored paths
class TreeNote():
    def __init__(self, state, parent, action):
        self.state = state    # current location 
        self.parent = parent  # previous note in path
        self.action = action  # action that got us to this location

def search(my_map):
    # Set the current state and mark the map location explored
    cur_loc = my_map.start
    my_map.mark(cur_loc, EXPLORED)
    cur_note = TreeNote(cur_loc, None, None)
    
    # Build a list on which to keep known but unexplored locations
    frontier = []
    
    while cur_loc != my_map.goal:    # search loop
        # What unexplored next steps are possible?
        moves = my_map.possible_moves(cur_loc, EXPLORED)
        
        # Add moves not already on the frontier to the frontier
        for a_move in moves:
            loc = my_map.simulate_move(cur_loc, a_move)
            if loc not in frontier:
                new_note = TreeNote(loc, cur_note, a_move)
                frontier.append(new_note)
                my_map.mark(loc, FRONTIER)
        
        # DEBUG: Uncomment to watch the frontier grow
        # print(my_map)
        # print(f'DEBUG: cur_loc = {cur_loc}; moves = {moves}')
        # print(f'DEBUG: frontier = {[note.state for note in frontier]}')
        # input('Ready to move on? ')
        
        if len(frontier) == 0:
            print('No solution')
            return
        
        # Choose a note from the frontier as next to explore
        next_note = frontier.pop()
        next_loc = next_note.state
        my_map.mark(next_loc, EXPLORED)
        
        # Update current state
        cur_note = next_note
        cur_loc = next_loc
    
    # Follow the parent links from cur_note to create
    # the actual driving directions
    ddirections = [cur_note]
    while cur_note.parent:  # while parent exists
        cur_note = cur_note.parent
        ddirections.insert(0, cur_note)
    
    # Print out the driving directions
    print('## Solution ##')
    print(f'Starting at {ddirections[0].state}')
    ddirections.pop(0)
    for n in ddirections:
        print(f'Go {n.action} then')
    print('Arrive at your goal')
    return

If you compare this code with directions0.py, you’ll see that the only differences are the creation of notes (lines 19 and 32), the maintenance of them on the frontier list (lines 33 and 47), and the determination and printing of the final driving directions (lines 55-68). In reviewing directions-dfs.py, pay careful attention to the difference between cur_note, new_note, and next_note. The first is a loop-carried variable, which we update at the end of the while-loop and use throughout the early part of the loop body. The others are just temporary names that we don’t want to overwrite the value in cur_note.

When search encounters the goal and the while-loop ends, the interpreter begins execution of the code on lines 55-68. These are the lines that use our notes to create the driving directions we desire. The first block (lines 55-60) starts with cur_note, which is the goal location when the while-loop exits, and builds a list (called ddirections) that reverses the order in which the loop visits the notes. The second block (lines 62-68) uses ddirections to print the actions in human-readable form. The only trickiness is on line 65 where we must remember to remove the note corresponding to the start location, which has no stored action.

You Try It

Run python3 directions-dfs.py. It prints the driving directions we desire!

Depth-first search (DFS). The search algorithm in directions-dfs.py is a depth-first search.

You Try It

Again uncomment lines 37-40 in directions-dfs.py and run python3 directions-dfs.py. It prints a sequence of maps corresponding to each step the function search makes. When you review these maps in order, you’ll notice that search goes down a road as far as it can before backing up and trying a different road. When it encounters an intersection, it chooses a direction through that intersection and keeps going.

This behavior is clearly not the only thing our search algorithm could have done, and if we want to do something different, we need to understand what caused this behavior. The answer is amazingly simple: the way in which we add elements to and remove them from the frontier list. The current code does the following:

• When we find a new unexplored location, we append it to the end of the frontier list (line 33).

• When we go to explore a new location, we pop one off the end of the frontier list (line 47). In Python, pop with no arguments removes the last item from the list.

Computer scientists like to talk about this behavior as “last-in, first-out” and to imagine it as operating like a stack (e.g., a stack of plates): The last one added to the stack is the first one taken off.

What’s good about this approach? Well, if we’re lucky, the first path we explore might lead to the goal state, and even if not, the approach can be very fast in finding a solution when there are many possible solutions. On the other hand, when there are many paths to the goal, this approach just takes the first it finds. There’s no guarantee that our DFS solution is the shortest path to the goal.

Breadth-first search (BFS). But what if we’re interested in finding the shortest path from start to goal (i.e., let’s change our specification). Can we change the way search operates to guarantee that it returns the shortest path, if one exists? We can, and what’s even more amazing is that it requires only a single character change!

You Try It

The only substantial difference between directions-dfs.py and directions-bfs.py is the addition of 0 as the parameter passed to pop (line 47). Line 1 is also different, but that change in the comment doesn’t affect the script’s behavior. Now uncomment lines 37-40 in directions-bfs.py and run it. Contrast how it explores the maze with what you saw when running directions-dfs.py.

Both versions of search place new unexplored locations at the end of the frontier list; they differ only in how they take unexplored locations from the frontier list. DFS takes from the end, and BFS, or breadth-first search, takes from the front. Instead of “last-in, first-out” as under DFS, BFS manages the frontier in a “first-in, first-out” manner, which is what computer scientists called a queue. Imagine the line that queues up to check-out at a grocery store.

When you watched the BFS script operate, you saw the search expand in all directions at the same rate. In other words, no explored path was more than one step longer than any other path. This means that search will find the shortest path (or technically, one of the shortest) from start to goal before any longer path. This approach is guaranteed to find the shortest path, but at the cost of searching methodically along every path.

You Try It

If you take the time to figure out how the configuration strings work in maze.py, design your own map, and then reference it on line 74 in the DFS and BFS scripts. You should find that these fairly short scripts are impressively robust!

Informed searches. Both DFS and BFS are called uninformed searches because they don’t use any information about the problem except what they gleam from their own explorations. This means that you can directly use these algorithms on any goal-directed search problem. You just need to encode your problem in a data structure comprising interconnected states, and then adapt the data-structure-specific parts of search to explore it!

But what if we were interested not in any goal-directed problem, but a specific one. Could we use information about the problem to create an algorithm that combines the direct-to-goal-nature of DFS with the good-answer-aspects of BFS? In other words, could problem-specific knowledge help us to identify and avoid paths that are unlikely to be a solution? As a concrete example, how might we adapt the goal-directed searches we’ve seen for the driving directions problem if we were given the as-the-crow-flies distance between each map location and the goal?

The as-the-crow-flies distance to the goal isn’t a set of driving directions (i.e., we’re not following the map!), but it does indicate which of two moves would bring us closer to the goal. Imagine using this distance to select the search algorithm’s next location from the frontier list. We’re using the distance to put the frontier list locations in a priority order. The higher the priority, the more likely that location will get us to the goal.

In general, prioritizing our possible search moves is the job of a heuristic function. The heuristic we use, of course, might be wrong. For example, we might have to drive in a direction away from the goal to find the road that will get us to it. Heuristics don’t guarantee that we’ll do better, but good ones, on average, find a near-optimal solution more quickly than our two uninformed solutions.

There are many heuristics in the domain of search. I asked you to imagine a common one (called greedy), which always takes the move from the frontier list with the best heuristic score. Another called A* search, which often provides more consistently good results, combines the cost of the path to the current point (e.g., the number of steps taken to get there) with the value of that point’s heuristic. Overall, there is a rich literature associated with search, and you are now prepared to dive into it to solve your own goal-directed search problems.

---

[1]

It didn’t take many years of Google’s existence before it realized that maps and mapping should an important part of its web services. As a fun look at the history of Google Maps and how middle-aged entrepreneurs working civilized hours launched what has become Maps, you might read this short Medium article: https://medium.com/@lewgus/the-untold-story-about-the-founding-of-google-maps-e4a5430aec92.

[2]

The challenge in designing algorithms and data structures is in discovering functional and data abstractions that are simultaneously: (1) easily understood by humans; (2) easily coded in an existing programming language; (3) easily executed by existing computers; and (4) easily mapped to real-world problems. Achieving all four isn’t easy, and an important reason to be familiar with classical algorithms and data structures is because they have been shown to exhibit all these features. Most of the time, problem solving with computation is about selecting which classical algorithms and data structures are problem-appropriate than it is about discovering entirely new algorithms and data structures.

[3]

To run the code blocks in this chapter, you’ll need to upload `maze.py` and `city.py` from the book’s GitHub repository into your IDE or interactive Python notebook session.

[4]

Yes, I’m having some fun with the name of our square-grid city. If you’ve tried to drive around Boston, you’ll know what I mean.

[5]

These string values are what `move` expects for its `direction` parameter. Capitalization doesn’t matter for these strings, and typing only the first letter is sufficient.

[6]

Using an emoji for my dog shows the limitations of ASCII art, which depends upon monospaced characters. Emoji don’t abide by monospacing. Please excuse the poor spacing caused by the dog face. I find it more fun to look at this emoji than a bland ‘s’ character.

[7]

The asterisk characters are printed to the terminal in blue because of the use of the escape codes you see in the definition of `EXPLORED` in `dogwalk.py`. You can learn more about these codes through an ALE in Chapter 6.

[8]

The `sim.py` and `dogwalk.py` were inspired by Program 1.4.4 in Robert Sedgewick and Kevin Wayne, Computer Science: An Interdisciplinary Approach (Boston, MA: Addison-Wesley, 2017), 113.

[9]

You might notice that the for-loop inside the `sim` function (line 16) names the loop variable `_`. This is another Python convention you’ll often see employed when we need a loop body to iterate a known number of times, but we don’t need the iteration count during the loop’s execution. The programmer is saying that the loop variable is intentionally unused.

[10]

Guttag, Introduction to Computation and Programming Using Python: With Application to Understanding Data, 177.

[11]

I don’t fault the designers of Python for not clearly separating interface from implementation. I’ve programmed in other languages that require a rigid interface specification, and I personally don’t think it helps. The syntax of a programming language simply is not a good place to try to explain a data type’s abstraction. Python’s approach is saying, in effect, that the interface is in the code that follows, but you probably want to read something in English to best understand it.

[12]

https://en.wikipedia.org/wiki/Google_Maps_pin

[13]

I show only `Pin.__init__`, which is spelled with two leading and two trailing underscore characters. In `city.py`, `CitySqGrid.__init__` does work appropriate for one of its instances. For instance, it makes sure that the city is between 2 and 20 buildings on a side and that this number is an even (so that there is a single central location).

[14]

A function within a class namespace is what is called a method.

[15]

While Python doesn’t require the name `self`, it is highly recommended that you follow this common practice. If you do, other Python programmers will immediately know what you’re doing.

[16]

As well as the values in `self.note`, `self.stars`, and `self.icon`.

[17]

Programming with class variables is tricky. If you’d like to learn more about them, I encourage you to read a book focused on the object-oriented properties of Python.

[18]

Nishant Gupta’s short Medium article titled “Understanding Python Property Decorators: Getters, Setters” describes the basics of how Python supports this pattern. https://medium.com/nishkoder/understanding-python-property-decorators-getters-setters-57d6b535e5d2

[19]

There’s nothing in Python stopping you from using, for example, the name `__distance__` except convention in the Python programming community. By following the convention, experienced Python programmers know what you’re doing.

[20]

This map closely resembles the one used in Week 0 (Search) of CS50’s Introduction to Artificial Intelligence with Python (https://cs50.harvard.edu/ai). I thank David Malan and his team for the use of it.